Решим задачу: в вазе лежат 6 яблок и 12 груш. Сколько в ней плодов? Ответ тривиален: 6 + 12 = 18. Если выбрать из вазы один лежащий в ней плод, то это можно сделать 18 способами. Вообще справедлив следующий принцип комбинаторики: если объект а можно выбрать m способами, а объект b выбрать n способами, то выбор “а или b” можно сделать m + n способами.
На языке теории множеств это утверждение означает, если
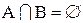 и
и 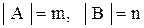 , то
, то
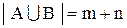 .
.
Сложнее получить ответ, когда А и В пересекаются.
Пусть 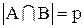 . Тогда, находя
. Тогда, находя 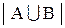 , мы к мощности (числу элементов) А прибавим число элементов в В, причем число элементов
, мы к мощности (числу элементов) А прибавим число элементов в В, причем число элементов 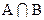 попадет в сумму дважды: один раз - в слагаемом
попадет в сумму дважды: один раз - в слагаемом 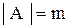 , второй - в слагаемом
, второй - в слагаемом 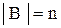 . Поэтому из
. Поэтому из 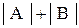 нужно один (лишний) раз
нужно один (лишний) раз 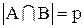 - вычесть.
- вычесть.
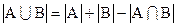 .
.
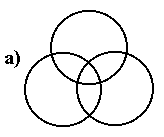 |
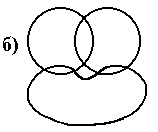 |
Разберемся в случае с тремя множествами. Если эти множества перекрываются лишь попарно (рис. б), то см. выше. Если 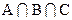 непусто (рис.а), то его элементы в случае см. выше окажутся совсем неучтенными: сначала их три раза учитывают, когда складывают мощности каждого из трех множеств А, В и С, а потом те же три раза учитывают, вычитая мощности пересечений множеств по два. Эти операции гасят друг друга, и полученный ответ окажется меньше истинного как раз на число элементов
непусто (рис.а), то его элементы в случае см. выше окажутся совсем неучтенными: сначала их три раза учитывают, когда складывают мощности каждого из трех множеств А, В и С, а потом те же три раза учитывают, вычитая мощности пересечений множеств по два. Эти операции гасят друг друга, и полученный ответ окажется меньше истинного как раз на число элементов 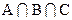 . Значит, это число и надо добавить.
. Значит, это число и надо добавить.
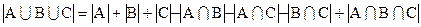 .
.
Общее правило для 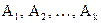 выглядит так:
выглядит так:
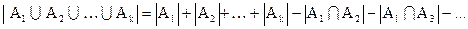
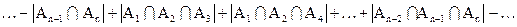
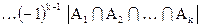 .
.
Пример: Во время отпуска 12 дней шел дождь, 8 дней дул сильный ветер, причем 5 дней были дождливы и ветренны. Сколько было дней с плохой погодой?
12 + 8 - 5 = 15.
 2015-06-28
2015-06-28 1220
1220








