Решим задачу: четыре цифры 1, 2, 3, 4 можно переставлять друг с другом 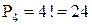 способами. В слове “мама” - 4 буквы. Но перестановок из этих букв можно составить не 24, а только 6:
способами. В слове “мама” - 4 буквы. Но перестановок из этих букв можно составить не 24, а только 6:
мама, маам, ммаа, амам, аамм, амма.
Чтобы понять, как это случилось, поставим в соответствие цифрам 1, 2 букву “м”, а 3 и 4 - “а”. Тогда, например, перестановке 1234 - “ммаа”, а 1324 - “мама”. Но слово “ммаа” соответствует не только перестановке 1234, но и 2134, 1243, 2143. Если цифры 1 и 2 меняются местами, то в соответствующем слове меняются местами две буквы “м”, следовательно, само слово остается неизменным. Таким образом, среди 24 перестановок 4 - х букв будут одинаковыми 2! тех, которые отличаются лишь сменой мест букв “м”, а также 2! тех, которые отличаются лишь переменой букв “а”. И тогда это число их:
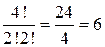 .
.
Пусть дан вектор длины n, составленный из элементов 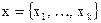 , причем
, причем 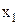 входит в вектор
входит в вектор 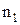 раз,
раз, 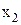 -
- 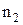 раза,...,
раза,..., 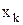 -
- 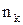 раз. Тогда
раз. Тогда
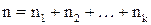 .
.
Если переставлять в этом векторе буквы, будут получаться новые векторы, имеющие тот же состав, т. е. буква 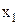 входит
входит 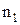 раз и т. д. Будем называть эти векторы перестановками с повторениями и букв
раз и т. д. Будем называть эти векторы перестановками с повторениями и букв 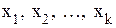 , имеющими состав
, имеющими состав 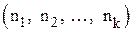 . Обозначим
. Обозначим 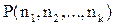 . По правилу произведения число перемещений букв, не меняющих данную перестановку, равно
. По правилу произведения число перемещений букв, не меняющих данную перестановку, равно 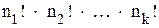 Но n элементов можно переставлять друг с другом n! способами. Поэтому число различных перестановок букв, имеющих состав
Но n элементов можно переставлять друг с другом n! способами. Поэтому число различных перестановок букв, имеющих состав 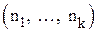 , в
, в 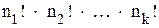 раз меньше, чем n!. Таким образом:
раз меньше, чем n!. Таким образом:
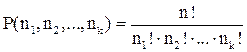 ,
,
где 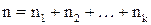 .
.
 2015-06-28
2015-06-28 404
404








