Утверждение (о взаимно однозначном соответствии равномощных множеств)

Если между конечными множествами А и В существует взаимно однозначное соответствие, то .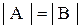

Доказательство: Действительно, если это не так, то либо 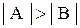и тогда, так как соответствие всюду определено, в А найдутся 2 элемента, которым соответствует один и тот же элемент 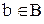, но тогда нарушена единственность прообраза либо; 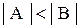и тогда, поскольку соответствие сюрьектвно, в В найдутся 2 элемента, соответствующие одному и тому же 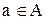, но тогда нарушена единственность образа.

Этот факт:

- позволяет установить равенство мощностей двух множеств, не вычисляя мощностей этих множеств;

- дает возможность вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется.

Для иллюстрации этого приема докажем теорему о числе подмножеств конечного множества.