Утверждение 1:
Множество 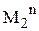 - счетно. Соответствие между N и
- счетно. Соответствие между N и 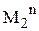 взаимно однозначно. Это было показано в примере.
взаимно однозначно. Это было показано в примере.
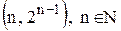 .
.
Утверждение 2:
Вообще любое бесконечное подмножество множества N - счетно.
Пояснение. Действительно, пусть 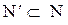 . Выберем в
. Выберем в 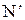 наименьший элемент и обозначим его за
наименьший элемент и обозначим его за 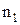 . В
. В 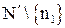 выберем наименьший элемент и обозначим его за
выберем наименьший элемент и обозначим его за 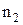 . В
. В 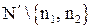 выберем наименьший элемент и обозначим его за
выберем наименьший элемент и обозначим его за 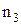 и т. д. Поскольку для всякого натурального числа имеется лишь конечное множество меньших натуральных чисел, то любой элемент из
и т. д. Поскольку для всякого натурального числа имеется лишь конечное множество меньших натуральных чисел, то любой элемент из 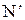 рано или поздно получит свой номер. Эта нумерация, то есть соответствие
рано или поздно получит свой номер. Эта нумерация, то есть соответствие 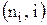 , и есть взаимно однозначное соответствие между
, и есть взаимно однозначное соответствие между 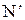 и N.
и N.
Утверждение 3:
Множество 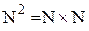 - счетно.
- счетно.
Пояснение. Нумерацию 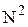 можно устроить следующим образом. Разобьем
можно устроить следующим образом. Разобьем 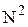 на классы. К первому классу
на классы. К первому классу 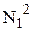 отнесем все пары чисел с наименьшей суммой, такая пара одна — (1, 1).
отнесем все пары чисел с наименьшей суммой, такая пара одна — (1, 1).
Ко второму классу 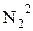 отнесем все пары чисел с суммой 3:
отнесем все пары чисел с суммой 3:
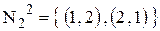 .
.
В общем случае 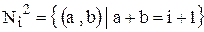 . Каждый класс содержит ровно i пар. Упорядочим теперь классы по возрастанию индексов i, а пары внутри класса по возрастанию первого элемента и занумеруем получившуюся последовательность номерами 1, 2, 3,... Очевидно, что если a+b = i+1, то пара (a,b) получит номер:
. Каждый класс содержит ровно i пар. Упорядочим теперь классы по возрастанию индексов i, а пары внутри класса по возрастанию первого элемента и занумеруем получившуюся последовательность номерами 1, 2, 3,... Очевидно, что если a+b = i+1, то пара (a,b) получит номер:
1+2 +... (i - 1) + a,
(где а – нумерация в классе 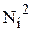 по возрастанию первого элемента пары, то есть по элементу а). Эта нумерация доказывает счетность
по возрастанию первого элемента пары, то есть по элементу а). Эта нумерация доказывает счетность 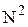 .
.
 2015-06-28
2015-06-28 647
647








