2015-06-28
2553
Если для конечного множества А,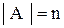 
, то число всех подмножеств А равно 
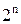, то есть 
.
Доказательство:
Занумеруем элементы А по номерам от 1 до n.
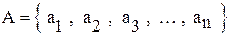
и рассмотрим множество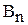 
двоичных векторов из нулей единиц длины n. Каждому подмножеству 
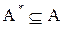поставим в соответствие вектор 
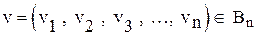следующим образом:
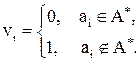
Например,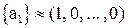 
,
,
,
.
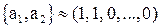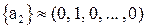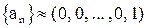Здесь и далее знаком “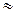 
” обозначено “соответствует”.
Например,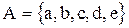 
, то подмножеству 
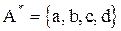соответствует вектор (1, 1, 1, 1, 0), а
.
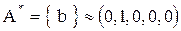Поэтому, подмножеству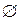 
соответствует вектор из нулей, а самому А - из единиц. Очевидно, что установленное соответствие между множеством всех подмножеств множества А и двоичными векторами длины n является взаимно однозначным, и число подмножеств А равно 
.
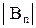А так как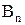 
является прямым произведением n двухэлементных множеств {0,1} (т. е. 
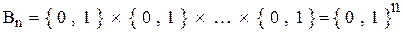), то, в силу следствия из теоремы о мощности прямого произведения множеств, имеем: 
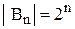так как 
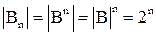, то есть 
.
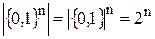Определение: Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие.
Для конечных множеств это утверждение доказывается. Для бесконечных множеств оно является определением равномощности.
Определение: Счетные множества это множества равномощные N (т. е. между ними и N можно установить взаимно однозначное соответствие).
