Задача 7. Решить систему линейных уравнений при помощи правила Крамера

Решить систему линейных уравнений при помощи правила Крамера:

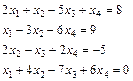
Правило Крамера заключается в следующем. Если определитель 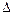= det A мат­рицы системы из п уравнений с п неизвестными Ах = b отличен от нуля (если определитель матрицы системы равен нулю, это не означает, что система не имеет решения; возможно ее нельзя решить по формулам Крамера), то система имеет единственное решение x_1,…. x₂,..., х_n, определяемое по формулам Крамера 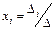, где 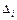- определитель матрицы, полученный из матрицы системы А заменой i- го столбца столбцом свободных членов b. Итак, для решения поставленной задачи необходимо выполнить следующие действия:

■ представить систему в матричном виде, то есть сформировать матрицу системы А и вектор правых частей b,

■ вычислить главный определитель ;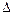

■ сформировать вспомогательные матрицы для вычисления определите­лей 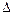_i;

■ вычислить определители ;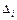

■ найти решение системы по формуле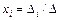

Фрагмент рабочего документа, приведенный в листинге 75, содержит ре­шение поставленной задачи.