Матричная норма- это некоторая скалярная числовая характеристика, которую ставят в соответствие матрице. В задачах линейной алгебры используются различные матричные нормы:
■ первая норма 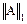 квадратной матрицы А =
квадратной матрицы А = 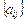 :
:
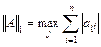
■ вторая норма 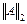 квадратной матрицы A = {аij}:
квадратной матрицы A = {аij}:
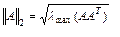
где 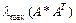 - максимальное собственное значение матрицы А;
- максимальное собственное значение матрицы А;
■ евклидова норма 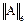 квадратной матрицы А =
квадратной матрицы А = 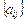 :
:
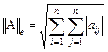
■ бесконечная норма 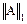 квадратной матрицы А:
квадратной матрицы А:
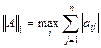
Число обусловленности матрицы А используется для определения меры чувствительности системы линейных уравнений Ах = b к погрешностям задания вектора b. Чем больше число обусловленности, тем более неустойчив процесс нахождения решения системы. Существует несколько вариантов нахождения числа обусловленности, но все они связаны с нормой матрицы и равны произведению нормы исходной матрицы на норму обратной:
■ число обусловленности матрицы, вычисленное в норме 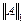 :
:
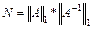
■ число обусловленности матрицы, вычисленное в норме 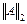 :
:
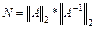
■ число обусловленности матрицы, вычисленное в норме 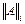 :
:
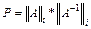
■ число обусловленности матрицы, вычисленное в норме 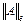
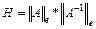
 2015-06-28
2015-06-28 1512
1512








