Теорема о противоположных векторах

Произведение вектора на 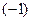есть вектор, противоположный вектору .

Доказательство. Действительно, ,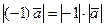

т.е. 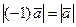и, кроме того,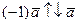

Утверждение доказано.

Вектор 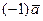обозначают 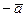. Введем теперь понятие разности двух векторов.

Определение. Разностью векторов и называется вектор, равный сумме вектора и вектора, противоположного вектору .

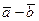Разность векторов и обозначается .По определению

.

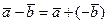Имеет место равенство 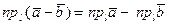, где - любая ось.

Если воспользоваться этой формулой, то нетрудно привести ещё одно доказательство, наряду с рассмотренным ранее, критерия равенства двух векторов. Рекомендуем проделать это самостоятельно.