2015-06-28
1171
Определение. Произведением вектора 
на скаляр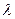 
называется вектор, модуль которого равен произведению модулей сомножителей, а направление совпадает с направлением вектора , если число 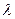положительно, и противоположно направлению вектора , если число 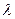отрицательно.
Произведение вектора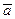 
на скаляр 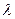обозначается 
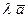или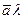 
. По определению:
1. 
;
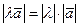2. 
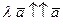, е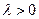сли 
, 
, если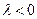 
;
3. если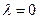 
, то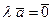 
;
4. если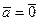 
, то .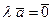
Согласно определению, произведение вектора на скаляр 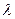есть вектор, коллинеарный вектору .
Теорема ( о проекции на ось произведения вектора на скаляр). Проекция на ось произведения вектора на скаляр равна произведению этого скаляра на проекцию рассматриваемого вектора на ту же ось, т.е.
,
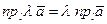где 
- любая ось.
Доказательство. По теореме о проекции вектора на ось
,
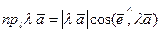где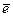 
- орт оси . Если в правой части этого равенства воспользоваться определением понятия модуля произведения вектора на скаляр, то получим
(*)
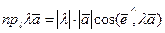При этом возможны следующие случаи:
1. .
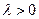В этом случае по определению модуля числа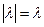 
. Кроме того, при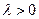 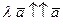, и поэтому 
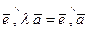. Следовательно, в силу равенства (*) имеем
|
|
|
.
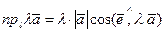Если теперь в правой части последнего равенства воспользоваться свойством сочетательности умножения чисел и применить теорему о проекции вектора на ось, то получим
.
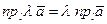2.
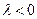
В этом случае по определению модуля числа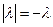 
. Кроме того, при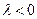 
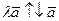, т.е. 
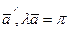и потому 
.
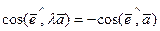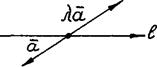
Исходя из равенства (*), приходим к выводу, что в рассматриваемом случае
,
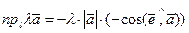и потому, как и при 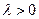, имеем
.
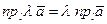В справедливости утверждения при 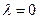предлагаем убедиться самостоятельно.
