1. Критерий линейной зависимости векторов. Для того, чтобы векторы 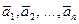 были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из этих векторов был представим в виде линейной комбинации всех остальных:
были линейно зависимыми, необходимо и достаточно, чтобы хотя бы один из этих векторов был представим в виде линейной комбинации всех остальных:
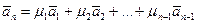 .
.
Мы выделили вектор 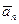 , но это не налагает никаких ограничений, так как всегда можно произвести перенумерацию векторов.
, но это не налагает никаких ограничений, так как всегда можно произвести перенумерацию векторов.
Доказательство
Необходимость. По условию 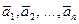 линейно зависимые векторы, и потому, по определению, существует такая совокупность чисел
линейно зависимые векторы, и потому, по определению, существует такая совокупность чисел 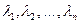 из которых хотя бы одно отлично от нуля, что справедливо равенство
из которых хотя бы одно отлично от нуля, что справедливо равенство
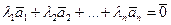 .
.
Пусть 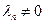 . Тогда, полагая
. Тогда, полагая 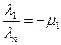 ;
; 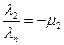 ; …;
; …; 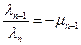 ,
,
получим 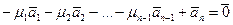 , то есть
, то есть 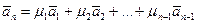 .
.
Достаточность. Пусть 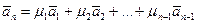 .
.
Тогда 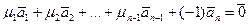 .
.
Очевидно, что по меньшей мере одно из чисел в линейной комбинации в левой части этого равенства отлично от нуля 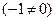 и потому, на основании определения, векторы
и потому, на основании определения, векторы 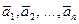 линейно зависимы.
линейно зависимы.
2. Если среди векторов 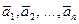 имеется нуль-вектор, то рассматриваемые векторы линейно зависимы.
имеется нуль-вектор, то рассматриваемые векторы линейно зависимы.
Доказательство. Пусть 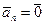 , тогда можно положить
, тогда можно положить 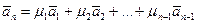 , где
, где 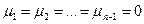 .
.
Следовательно, векторы 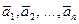 , согласно критерию, линейно зависимы.
, согласно критерию, линейно зависимы.
3. Если в совокупности векторов 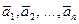 векторы
векторы 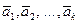
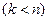 являются линейно зависимыми, то и векторы
являются линейно зависимыми, то и векторы 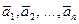 линейно зависимы.
линейно зависимы.
Доказательство. Действительно, если 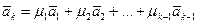 , то
, то 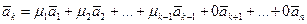
и потому, согласно критерию, векторы 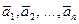 линейно зависимы.
линейно зависимы.
Теорема (об одинаково направленных векторах). Если векторы  и
и  одинаково направлены, то
одинаково направлены, то 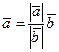 .
.
При этом разумеется, что 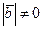 .
.
Доказательство. Надо показать, что если 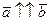 и
и 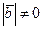 , то векторы
, то векторы 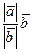 и
и  равны. Действительно,
равны. Действительно,  , т.е. модули векторов
, т.е. модули векторов 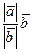 и
и  равны. Далее,
равны. Далее, 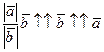 .
.
Следовательно, направления векторов 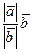 и
и  совпадают. Теорема доказана.
совпадают. Теорема доказана.
Теорема (о противоположно направленных векторах). Если векторы 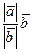 и
и  противоположно направлены, то
противоположно направлены, то 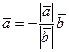
При этом разумеется, что 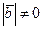 .
.
Доказательство. Надо показать, что если 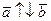 и
и 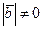 , то векторы
, то векторы 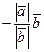 и
и  равны. Действительно,
равны. Действительно, 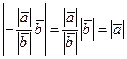 , т.е. модули векторов
, т.е. модули векторов 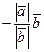 и
и  равны. Далее,
равны. Далее, 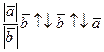 . Следовательно, направления векторов
. Следовательно, направления векторов 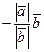 и
и  совпадают. Утверждение доказано.
совпадают. Утверждение доказано.
Теорема (о связи между вектором и его ортом). Всякий ненулевой вектор может быть представлен в виде произведения модуля этого вектора на его орт:
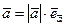
Доказательство. Воспользуемся теоремой об одинаково направленных векторах. По определению 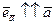 и потому
и потому 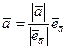 .
.
Так как 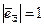 , то для любого ненулевого вектора справедливо равенство
, то для любого ненулевого вектора справедливо равенство
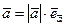 ,
,
что и требовалось доказать.
Следствие. Для орта ненулевого вектора справедливо равенство
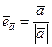 .
.
Теорема (о связи между составляющей вектора по оси и ортом этой оси). Составляющая вектора по оси равна произведению проекции рассматриваемого вектора на ось и орта той же оси, т.е.
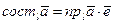
где  - любая ось,
- любая ось, 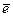 - орт этой оси.
- орт этой оси.
Доказательство. Проведем доказательство в предположении, что 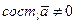 Согласно теореме о связи между вектором и его ортом,
Согласно теореме о связи между вектором и его ортом, 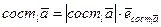 .
.
При этом возможны следующие случаи:
1. 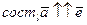 .
.
Тогда по определению проекции вектора на ось 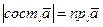 . Кроме того
. Кроме того 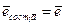 . Следовательно,
. Следовательно, 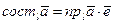 .
.
2. 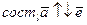
Тогда 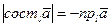 и
и 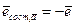 . Значит,
. Значит, 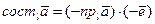 . Таким образом
. Таким образом 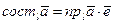 , что и требовалось доказать.
, что и требовалось доказать.
Справедливость рассматриваемого утверждения в том случае, когда 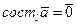 (есть нуль-вектор), рекомендуем проверить самостоятельно.
(есть нуль-вектор), рекомендуем проверить самостоятельно.
 2015-06-28
2015-06-28 1916
1916
