Определение. Линейной комбинацией векторов 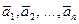 с числами
с числами 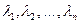 , называется вектор
, называется вектор 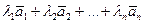
Определение. Векторы 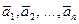 называются линейно-зависимыми, если существует такая совокупность действительных чисел
называются линейно-зависимыми, если существует такая совокупность действительных чисел 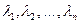 , из которых хотя бы одно отлично от нуля (
, из которых хотя бы одно отлично от нуля (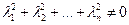 ), что линейная комбинация векторов
), что линейная комбинация векторов 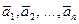 с указанными числами есть нуль-вектор:
с указанными числами есть нуль-вектор:
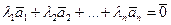 .
.
Определение. Векторы 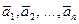 называются линейно независимыми, если линейная комбинация этих векторов с действительными числами
называются линейно независимыми, если линейная комбинация этих векторов с действительными числами 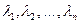 есть нуль-вектор только в том случае, когда все числа
есть нуль-вектор только в том случае, когда все числа 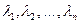 равны нулю:
равны нулю:
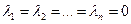 .
.
 2015-06-28
2015-06-28 418
418








