2015-06-28
1330
1. Сложение векторов обладает свойством переместительности:
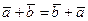
Доказательство. Для того, чтобы доказать, что векторы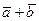 
и 
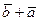равны, достаточно доказать, что равны проекции этих векторов на любую ось. Пусть 
- произвольная ось. По теореме о проекции суммы двух векторов на ось
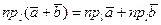и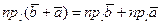 
Учитывая свойство переместительности сложения чисел, имеем
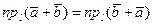
где - любая ось и потому, на основании критерия равенства двух векторов, .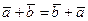
2. Сложение векторов обладает свойством сочетательности, т.е.
.
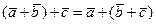Доказательство. Для того, чтобы доказать, что векторы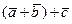 
и 
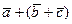равны, достаточно доказать, что равны проекции этих векторов на любую ось. Пусть - произвольная ось. Применим теорему о проекции суммы двух векторов на ось:
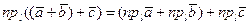
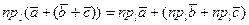
Учитывая свойство сочетательности сложения чисел, имеем
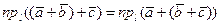
где - любая ось. Следовательно, по критерию равенства векторов,
.
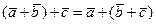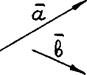
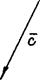
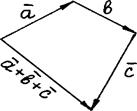Определение. Суммой конечного числа векторов называется вектор, началом которого является начало первого из складываемых векторов, а концом - конец последнего, при этом разумеется, что начало каждого из складываемых векторов, начиная со второго, совмещено с концом предыдущего.
Теорема (о проекции суммы векторов на ось). Проекция суммы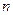 
векторов на любую ось равна сумме проекций складываемых векторов на ту же ось, т.е.
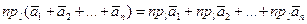
где - произвольная ось.
Теорема легко может быть доказана методом математической индукции с учетом ранее доказанной теоремы о проекции суммы двух векторов на любую ось.
