2015-06-28
259
Для того, чтобы векторы 
и 
были коллинеарны, необходимо и достаточно, чтобы векторное произведение векторов и было нуль-вектором:
| Векторы и коллинеарны
|  
| 
|
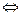
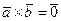
Доказательство. Необходимость. Пусть и коллинеарные векторы. Тогда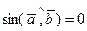 
. По определению модуля векторного произведения двух векторов 
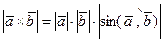, и потому 
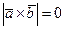, то есть .
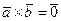Достаточность. Пусть 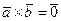, или, что то же самое, 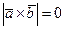. Тогда имеем 
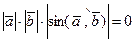. Отсюда следует, что пр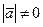и 
и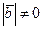 
имеет место равенство 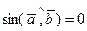, то есть векторы и коллинеарны. Критерий доказан.
КРИТЕРИИ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ВЕКТОРОВ
