Площадь треугольника 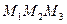 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 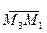 и
и 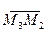 , и потому
, и потому
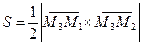 ,
,
где через 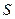 обозначена площадь треугольника
обозначена площадь треугольника 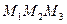 .
.
Применим теорему о представлении векторного произведения двух векторов через проекции перемножаемых векторов на координатные оси и теорему о проекции вектора на числовую ось.
Тогда для площади треугольника с вершинами в точках 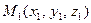 ,
, 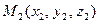 ,
, 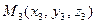 получим
получим
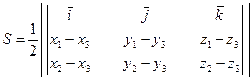
или
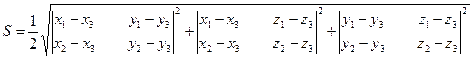
Площадь треугольника с вершинами в точках 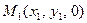 ,
, 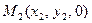 ,
, 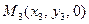 может быть вычислена по формуле
может быть вычислена по формуле
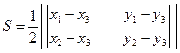
или, что то же самое,
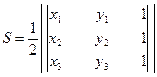 .
.
 2015-06-28
2015-06-28 276
276








