Для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы сумма произведений одноименных проекций этих векторов на координатные оси была равна нулю:
   |  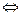 | 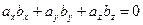 |
Доказательство. Справедливость этого утверждения с очевидностью вытекает из теоремы о представлении скалярного произведения двух векторов через проекции этих векторов на координатные оси и первого критерия перпендикулярности двух векторов.
КРИТЕРИИ КОМПЛАНАРНОСТИ ТРЁХ ВЕКТОРОВ
Первый критерий компланарности трёх векторов
Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы смешанное произведение этих векторов было равно нулю:
Векторы  , ,  , ,  компланарны компланарны |  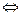 | 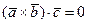 |
Доказательство. Необходимость. Пусть векторы  ,
,  ,
,  компланарны, следовательно, по определению, существует плоскость, которой эти векторы параллельны. Вектор
компланарны, следовательно, по определению, существует плоскость, которой эти векторы параллельны. Вектор 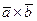 , по определению, перпендикулярен каждому из векторов
, по определению, перпендикулярен каждому из векторов  и
и  . Значит, вектор
. Значит, вектор 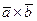 перпендикулярен вектору
перпендикулярен вектору  , и потому, согласно первому критерию перпендикулярности векторов,
, и потому, согласно первому критерию перпендикулярности векторов, 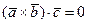 .
.
Достаточность. Пусть 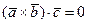 , тогда
, тогда 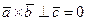 . Если, кроме того, учесть, что вектор
. Если, кроме того, учесть, что вектор 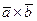 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и  , то придем к выводу, что векторы
, то придем к выводу, что векторы  ,
,  ,
,  компланарны.
компланарны.
Второй критерий компланарности трёх векторов
Для того, чтобы векторы  ,
,  ,
,  были компланарны, необходимо и достаточно, чтобы выполнялось равенство
были компланарны, необходимо и достаточно, чтобы выполнялось равенство
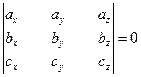 .
.
Доказательство. Справедливость этого утверждения вытекает из предыдущего критерия с учетом теоремы о представлении смешанное произведения трёх векторов через их проекции на координатные оси.
Третий критерий компланарности трёх векторов
Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы они были линейно зависимы:
Векторы  , ,  , ,  компланарны компланарны |   | Векторы  , ,  , ,  линейно зависимы линейно зависимы |
Доказательство. Необходимость. Для того, чтобы показать, что векторы  ,
,  ,
,  линейно зависимы докажем, что если векторы
линейно зависимы докажем, что если векторы  и
и  неколлинеарны, то существуют такие действительные числа
неколлинеарны, то существуют такие действительные числа 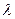 и
и 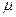 , что
, что
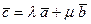 .
.
Векторы  ,
,  ,
,  предполагаются компланарными и потому можно считать, что
предполагаются компланарными и потому можно считать, что 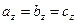 . Итак, докажем, что если векторы
. Итак, докажем, что если векторы  и
и  неколлинеарны, то существуют такие действительные числа
неколлинеарны, то существуют такие действительные числа 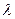 и
и 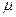 , что
, что
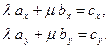 (1)
(1)
Если
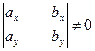 , (2)
, (2)
то, в силу теоремы Крамера, система (1) однозначно определяет 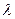 и
и 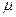 . В этом случае векторы
. В этом случае векторы  ,
,  ,
,  линейно зависимы.
линейно зависимы.
Условие (2) означает, что векторы  и
и  неколлинеарны.
неколлинеарны.
Если же
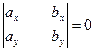 , то, учитывая, кроме того, что
, то, учитывая, кроме того, что 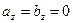 , получим
, получим 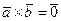 .
.
А отсюда следует, что векторы  и
и  коллинеарны, а, следовательно,
коллинеарны, а, следовательно,
линейно зависимы и потому векторы  ,
,  ,
,  линейно зависимы.
линейно зависимы.
Достаточность. Если векторы  ,
,  ,
,  линейно зависимы, то хотя бы один из них можно выразить в виде линейной комбинации с действительными числами двух других векторов. Положим
линейно зависимы, то хотя бы один из них можно выразить в виде линейной комбинации с действительными числами двух других векторов. Положим 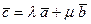 .
.
Тогда 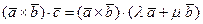 или
или 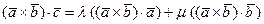
Учитывая, что 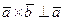 и
и 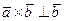 , получим
, получим 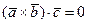 , и потому, согласно первому критерию компланарности трёх векторов, векторы
, и потому, согласно первому критерию компланарности трёх векторов, векторы  ,
,  ,
,  компланарны, что и требовалось доказать.
компланарны, что и требовалось доказать.
22. ТЕОРЕМА О ЛИНЕЙНОЙ ЗАВИСИМОСТИ ЛЮБЫХ n+1 ВЕКТОРОВ В n-МЕРНОМ ПРОСТРАНСТВЕ
Любые 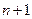 векторов в
векторов в 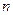 -мерном пространстве линейно зависимы.
-мерном пространстве линейно зависимы.
Доказательство. Мы рассмотрим теорему для 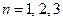 .
.
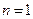 . В одномерном пространстве любые два вектора коллинеарны и потому линейно зависимы.
. В одномерном пространстве любые два вектора коллинеарны и потому линейно зависимы.
 . В двумерном пространстве любые три вектора компланарны и потому линейно зависимы.
. В двумерном пространстве любые три вектора компланарны и потому линейно зависимы.
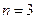 . Для того чтобы доказать, что в трёхмерном пространстве любые четыре вектора
. Для того чтобы доказать, что в трёхмерном пространстве любые четыре вектора  ,
,  ,
,  ,
, 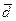 линейно зависимы, покажем, что если векторы
линейно зависимы, покажем, что если векторы  ,
,  и
и  некомпланарны, то существуют такие действительные числа
некомпланарны, то существуют такие действительные числа 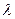 ,
, 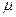 и
и 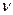 , что
, что 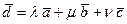 , то есть покажем, что если векторы
, то есть покажем, что если векторы  ,
,  и
и  некомпланарны, то существуют такие действительные числа
некомпланарны, то существуют такие действительные числа 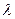 ,
, 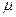 и
и 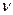 , что
, что
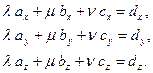 (1)
(1)
Если
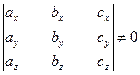 , (2)
, (2)
то в силу теоремы Крамера, система (1) однозначно определяет 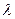 ,
, 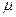 и
и 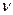 . В этом случае векторы
. В этом случае векторы  ,
,  ,
,  и
и 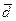 линейно зависимы.
линейно зависимы.
Условие (2) означает, что векторы  ,
,  и
и  некомпланарны. Если же
некомпланарны. Если же
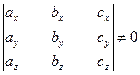 , (3)
, (3)
то векторы  ,
,  и
и  компланарны, а, следовательно, линейно зависимы и потому векторы
компланарны, а, следовательно, линейно зависимы и потому векторы  ,
,  ,
,  и
и 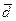 линейно зависимы.
линейно зависимы.
 2015-06-28
2015-06-28 2480
2480
