Общая постановка одноиндексных задач

1.1.1. Задача использования ресурсов

Пример 1. Для производства 3^х видов изделий А,В,С используется 3 различных вида сырья, каждый вид сырья может быть использован в количестве соответственно не больше 180;210;244 кг. Нормы затрат на 1ед. продукции данного вида и цена на 1ед. продукцию каждого вида приведены в табл.1:

Таблица 1

Виды сырья	А	В	С
1	4	2	1
2	3	1	3
3	1	2	5
Цена 1ед. продукции	10	14	12

Определить план выпуска продукции, при котором прибыль предприятия от реализации всех изделий будет максимальной. Составить матричную модель.

Решение. Пусть x₁ количество изделий вида А, x₂ – В, x₃ – С.

F = 10х₁ + 14х₂ + 12х₃ à max.

Ограничения по видам сырья:

4x₁ + 2x₂ + x₃ ≤ 180

3x₁ + x₂ + 3x₃ ≤ 210

x₁ + 2x₂ + 5x₃ ≤ 244

х₁ ≥ 0, х ₂≥ 0, х₃ ≥ 0

Пример 2. Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (табл. 2). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1- го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида. Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.

Таблица 2

	Расход инградиентов, т ингр./т краски
Ингредиенты	Краска 1-го вида	Краска 2-го вида	Запас, т
А
В

Решение: пустьx₁ – суточный объем производства краски 1-го вида, [т краски/сутки]; x₂ – суточный объем производства краски 2-го вида, [т краски/сутки].

F(X) = 3x₁ + 2x₂ → max [тыс. руб./сутки],

x₁ + 2x₂ ≤ 6 - ограничения по расходу А

2x₁ + x₂ ≤ 8 - ограничения по расходу В

x₂ - x₁ ≤ 1 - ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го

x₂ ≤ 2 - ограничение по суточному объему производства краски 2-го

x₁ ≥ 0, x₂ ≥ 0

В общем виде: пусть предприятие имеет m- видов ресурсов в количестве b_i единиц (i = 1,¯m), из которых производится n видов продукции. Для производства единицы j продукции расходуется a_ij единиц одного ресурса, а ее стоимость составляет c_j единиц. Составить план выпуска продукции x_i, обеспечивающий максимальную прибыль при наименьших затратах.

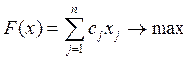(1)

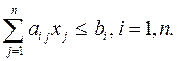(2)

х_j ≥ 0 (3)

1.1.2. Задача составления рациона

Пример 3. Имеется два вида корма, содержащие питательные вещества S₁, S₂, S₃. Содержание числа питательных веществ в 1кг. каждого вида корма и необходимый минимум питательных веществ приведены в табл. 3:

Таблица 3

	min	I	II
S1	9	3	1
S2	8	1	2
S3	12	1	6

Стоимость 1кг. корма 1 и 2 соответственно равны 4 и 6 руб. Необходимо составить дневной рацион, имеющий наименьшую стоимость, в котором содержания каждого вида питательных веществ было бы не менее установленного предела.

Решение: x_j — количество кормов 1 и 2 вида.

F = 4x₁+6x₂ à min.

3x₁ + x₂ ≥ 9

x₁ + 2x₂ ≥ 8

x₁ + 6x₂ ≥ 12

x_j ≥ 0

Пример 4. Фармацевтическая фирма ежедневно производит 800 фунтов некоторой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в табл.4.

Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов.

Таблица 4

Мука	Белок	Клетчатка	Стоимость (в долл. за фунт)
(в фунтах на фунт муки)
Кукурузная	0,09	0,02	0,3
Соевая	0,6	0,06	0,9

Решение: x_j – количество кукурузной и соевой муки. Стоимость пищевой добавки равна 0,3х₁ +0,9х₂. Так как белка в пищевой добавке не менее 30% от общей смеси, то:

0,09х₁ + 0,6х₂ ≥ 0,3*(х₁ +х₂) или 0,21х₁ – 0,3х₂ ≤ 0.

Аналогично, для соевой муки: 0,02х₁ + 0,06х₂ ≤ 0,05*(х₁ + х₂) или 0,03х₁ – 0,01х₂ ≥ 0. В результате получим:

F = 0,3х₁ +0,9х₂ → min

х₁ +х₂ ≥ 800

0,21х₁ – 0,3х₂ ≤ 0

0,03х₁ – 0,01х₂ ≥ 0

x_j ≥ 0

В общем виде: x_j – число j -го сырья в смеси (j = 1,¯m); b_i – необходимый минимум i -го ингредиента, содержащегося в единице смеси (i = 1¯,n); a_ij – количество ингредиента i, содержащегося в единице j -го вида; c_j – стоимость единицы j -го сырья; q – минимальный общий вес смеси, используемый фирмой. Найти такой рацион x_j, удовлетворяющий системе

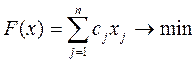
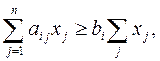
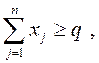
х_j ≥ 0.

1.1.3. Раскрой материала

Пример 5. Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскроя ткани. В табл. 5 приведены характеристики вариантов раскроя 10 м² ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405 м². В ближайший месяц планируется сшить 90 изделий. Постройте математическую модель задачи, позволяющую в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.

Таблица 5

Вариант раскроя	Количество деталей, шт./отрез	Отходы, м2/отрез
							0,5
							0,25
Комплектность, шт./изделие

Решение: пустьx₁ – количество отрезов ткани по 10 м², раскроенных первым способом в течение месяца, x₂ – количество отрезов ткани по 10 м², раскроенных вторым способом в течение месяца. F(X) = 0,5x₁ + 0,25x₂ → min

х₁ + x₂ ≤ 405/10 - общее количество ткани, раскроенной за месяц

60x₁ + 80x₂ ≥ 90 - общее количество деталей №1

35x₂ ≥ 180 - общее количество деталей №2

90x₁ + 20x₂ ≥ 180 - общее количество деталей №3

40x₁ + 78x₂ ≥ 180 - общее количество деталей №4

70x₁ +15x₂ ≥ 180 - общее количество деталей №5

90x₁ ≥ 180 - общее количество деталей №6

x₁ ≥ 0, x₂ ≥ 0.

Пример 6. Для производства брусьев длинной 1,2; 3 и 5 м в соотношении 2:1:3 на распил поступило 195 бревен длинной 6 м. Определить план распила, обеспечивающий максимальное число комплектов.

Решение: составим план раскроя

Таблица 6

Способы раскроя					Соотношения
1,2 м
3 м
5 м

Пусть х_i – количество бревен i- го распила, х – число комплектов брусьев. Тогда F = х → max

5х₁ + 2х₄ = 2х

2х₂ + х₄ = х

х₃ = 3х

х₁ + х₂ + х₃ + х₄ = 195

√x_i ≥ 0

В общем виде:

а) x_j – число единиц материала, раскраиваемых i-м способом,и х – число изготавливаемых комплектов изделий. На раскрой (распил) поступает материал одного образца в количестве a единиц, т.е. 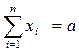. Требуется изготовить l разных комплектующий изделий в количествах, пропорциональным числам b₁, b₂,…, b_l (условие комплектности), если каждая единица материала может быть раскроена n различными способами, причем использование i -го способа (i = 1,¯n) дает a_ij единиц k -го (k = 1,¯l) изделия: 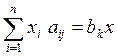(k = 1,¯l). Найти такой план раскроя x_i > 0, при котором целевая функция F = x принимает максимальное значение.

б) x_ij – число единиц j -го материала, раскраиваемых i-м способом,и х – число изготавливаемых комплектов изделий. На раскрой (распил) поступает материал m образцов в количестве a_j единиц, т.е. 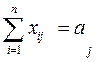(j = 1,¯m). Каждая единица j -го материала может быть раскроена n различными способами, причем использование i -го способа (i = 1,¯n) дает a_ijk единиц k -го (k = 1,¯l) изделия: 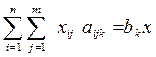(k = 1,¯l). Найти такой план раскроя x_ij > 0, при котором целевая функция F = x принимает максимальное значение.