Определение. Декартовой системой координат на плоскости называется совокупность двух перпендикулярных числовых осей с общим началом.
Точка 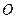 − начало выбранной системы координат на плоскости. Ось
− начало выбранной системы координат на плоскости. Ось 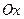 (ось абсцисс) и
(ось абсцисс) и 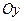 (ось ординат) − координатные оси;
(ось ординат) − координатные оси; 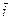 − орт оси
− орт оси 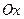 ,
, 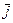 − орт оси
− орт оси 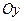 . Впредь будем предполагать, что координатные оси ориентированы так, что
. Впредь будем предполагать, что координатные оси ориентированы так, что 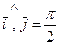 .
.
Координатные оси делят плоскость на четыре части, называемые квадрантами.
Пусть 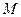 − произвольная точка на плоскости.
− произвольная точка на плоскости.
Определение. Радиусом-вектором точки 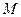 в выбранной декартовой системе координат называется вектор, началом которого является точка
в выбранной декартовой системе координат называется вектор, началом которого является точка 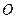 , а концом − точка
, а концом − точка 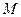 .
.
Из определения очевидно, что радиус-вектор точки 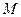 − закрепленный вектор.
− закрепленный вектор.
Определение. Абсциссой точки 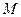 в выбранной декартовой системе координат называется проекция радиуса-вектора этой точки на ось абсцисс.
в выбранной декартовой системе координат называется проекция радиуса-вектора этой точки на ось абсцисс.
Абсциссу точки 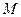 будем обозначать буквой
будем обозначать буквой 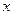 . По определению
. По определению
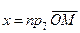 .
.
Определение. Ординатой точки 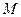 в выбранной декартовой системе координат называется проекция радиуса-вектора этой точки на ось ординат.
в выбранной декартовой системе координат называется проекция радиуса-вектора этой точки на ось ординат.
Ординату точки 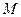 , будем обозначать буквой
, будем обозначать буквой 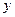 . По определению
. По определению
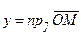 .
.
Определение. Пара чисел называется упорядоченной, если указано, какое из этих чисел - первое и какое - второе.
Можно доказать, что между множеством точек на плоскости и множеством упорядоченных пар вещественных чисел существует взаимнооднозначное соответствие.
Определение. Декартовыми координатами точки 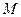 на плоскости в выбранной декартовой системе координат называется упорядоченная пара чисел
на плоскости в выбранной декартовой системе координат называется упорядоченная пара чисел 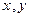 , т.е. абсцисса и ордината точки
, т.е. абсцисса и ордината точки 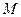 .
.
При этом обычно употребляется следующая запись: 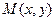 .
.
 2015-06-28
2015-06-28 1201
1201
