Графическая интерпретация множеств и операций над ними

Для графической интерпретации множеств используют диаграммы Венна, которые имеют следующий вид:

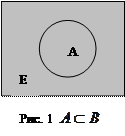
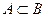
Над множествами выполняются три двуместные операции:

· Пересечение;

· Объединение;

· Разность множеств.

Пересечением множеств А и В (мультипликативная операция) называется новое множество С, которое включает в себя элементы принадлежащие и множеству А и множеству В.

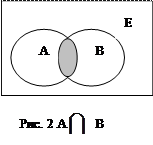
А 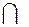В

Пример: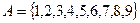

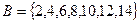
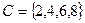
Объединением множеств А и В (аддитивная операция) называется новое множество С, состоящее из элементов множества А и из элементов множества В.

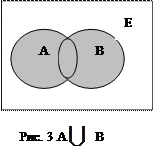
А 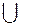В

Пример: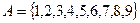

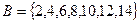
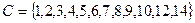
Разностью множеств А и В называется новое множество С, состоящее из элементов, принадлежащих множеству А и не принадлежащих множеству В.

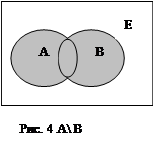
А\ В из А вычесть В

Пример: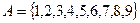

.

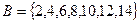
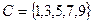Кроме рассмотренных двухместных операций существует одна одноместная операция – дополнение. Дополнением множества М является множество 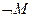(не М) = .

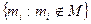Порядок выполнения операций: сначала выполняется одноместная операция дополнения, затем операция пересечения, затем операция объединения и операция разности. Для изменения этого порядка в выражении используют скобки.