П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения

Пусть известна плотность распределения f (x, y) случайного вектора. Согласно свойству 1 (условие согласованности) для функции распределения F (x, y): F (x, +∞) = F ₁(x), F (+∞, y) = F ₂(y), можем записать, что,

F ₁(x) = 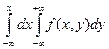, F ₂(y) = .

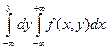Отсюда, дифференцированием первого равенства по х, а второго по y, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:

, .

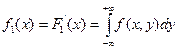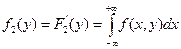Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.

Определение 9. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.

Теорема. Для того, чтобы дискретные случайные величины X и Y, входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:

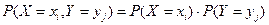
или p_ij = p_i p_j.

Для того, чтобы непрерывные случайные величины X и Y, входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:

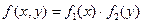или .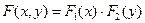

Пример 8. Дана плотность распределения непрерывного вектора: 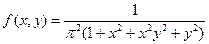. Зависимы или независимы случайные величины, входящие в систему?