Определение. Начальным моментом порядка 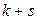 системы двух случайных величин
системы двух случайных величин  называется действительное число
называется действительное число 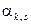 , определяемое по формуле:
, определяемое по формуле:
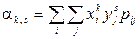 ,
,
если  – система двух дискретных случайных величин;
– система двух дискретных случайных величин;
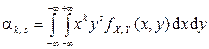 ,
,
если  – система двух непрерывных случайных величин.
– система двух непрерывных случайных величин.
Определение. Центральным моментом порядка 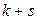 системы двух случайных величин
системы двух случайных величин  называется действительное число
называется действительное число 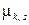 , определяемое по формуле:
, определяемое по формуле:
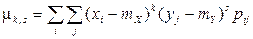 ,
,
если  – система двух дискретных случайных величин;
– система двух дискретных случайных величин;
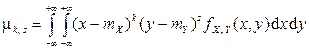 ,
,
если  – система двух непрерывных случайных величин.
– система двух непрерывных случайных величин.
На практике чаще всего встречаются моменты первого и второго порядков. Очевидно, что начальные моменты первого порядка есть не что иное, как математические ожидания компонент X и Y:
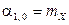 ,
, 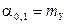 .
.
Точка с координатами 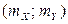 на плоскости xOy представляет собой характеристику положения случайной точки
на плоскости xOy представляет собой характеристику положения случайной точки  , а ее рассеивание (разброс) происходит вокруг
, а ее рассеивание (разброс) происходит вокруг 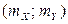 .
.
Центральные моменты первого порядка, очевидно, равны нулю, т.е.
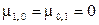 .
.
Имеются три начальных момента второго порядка – 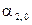 ,
, 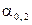 и
и 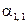 . Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:
. Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:
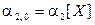 ,
, 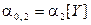 .
.
Имеются три центральных момента второго порядка 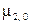 ,
, 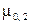 и
и 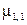 . Первые два из них представляют собой дисперсии компонент X и Y соответственно:
. Первые два из них представляют собой дисперсии компонент X и Y соответственно:
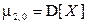 ,
, 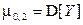 .
.
Рассмотрим 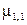 отдельно.
отдельно.
Определение. Центральный момент второго порядка 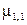 называется ковариацией случайной величины
называется ковариацией случайной величины  .
.
Для момента 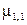 используется обозначение
используется обозначение 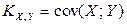 .
.
Замечание. По определению ковариации: 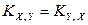 .
.
В механической интерпретации, когда распределение вероятностей на плоскости xOy трактуется как распределение единичной массы на этой плоскости, точка 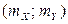 есть не что иное, как центр масс распределения; дисперсии
есть не что иное, как центр масс распределения; дисперсии 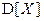 и
и 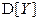 – моменты инерции распределения относительно точки
– моменты инерции распределения относительно точки 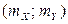 в направлении осей Ox и Oy соответственно, а ковариация – это центробежный момент инерции распределения масс.
в направлении осей Ox и Oy соответственно, а ковариация – это центробежный момент инерции распределения масс.
Теорема. Если случайные величины X и Y независимы, то 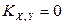 .
.
Замечание. Как правило, 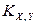 удобнее вычислять по формуле
удобнее вычислять по формуле
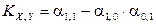 .
.
Ковариация 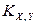 характеризует не только степень зависимости двух случайных величин
характеризует не только степень зависимости двух случайных величин  , но также их рассеивание вокруг точки
, но также их рассеивание вокруг точки 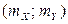 . Однако размерность ковариации
. Однако размерность ковариации 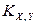 равна произведению размерностей случайных величин X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс, ковариацию
равна произведению размерностей случайных величин X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс, ковариацию 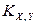 делят на произведение
делят на произведение 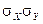 :
:
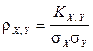 .
.
Определение. Величина 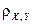 называется коэффициентом корреляции случайных величин X и Y.
называется коэффициентом корреляции случайных величин X и Y.
Коэффициент корреляции 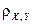 характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае
характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае 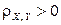 и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае
и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае 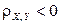 и говорят, что случайные величины X и Y связаны отрицательной корреляцией. Модуль коэффициента корреляции случайных величин X и Y характеризует степень тесноты линейной зависимости между ними. Если линейной зависимости нет, то
и говорят, что случайные величины X и Y связаны отрицательной корреляцией. Модуль коэффициента корреляции случайных величин X и Y характеризует степень тесноты линейной зависимости между ними. Если линейной зависимости нет, то 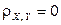 .
.
Теорема. Если случайные величины X и Y связывает линейная зависимость 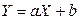 , то
, то 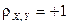 при
при 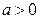 ,
, 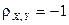 при
при 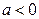 .
.
Пример 2.2.14. Найти коэффициент корреляции 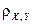 между случайными величинами: 1) X и
между случайными величинами: 1) X и 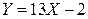 ; 2) X и
; 2) X и 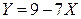 .
.
Решение. Согласно теореме 3.5.2: 1) 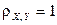 , т.к.
, т.к. 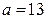 ,
, 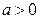 ; 2)
; 2) 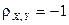 , т.к.
, т.к. 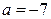 ,
, 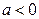 .
.
Ответ: 1) 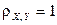 ; 2)
; 2) 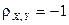 .
.
Пример 2.2.15. Игральная кость размечена таким образом, что сумма очков на противоположных гранях равна 7 (т.е. 1 и 6, 2 и 5, 3 и 4). Пусть X – число очков на верхней грани, Y – число очков на нижней грани. Построить совместный закон распределения случайных величин X и Y, найти коэффициент корреляции между ними.
Решение. По условию задачи 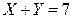 . Поэтому
. Поэтому 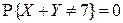 . Следовательно, для построения таблицы распределения случайного вектора
. Следовательно, для построения таблицы распределения случайного вектора  остается вычислить вероятности:
остается вычислить вероятности:
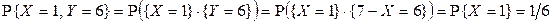 ,
,
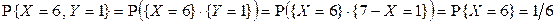 .
.
Аналогично можно показать, что
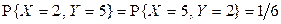 ,
, 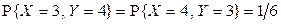 .
.
Тогда закон распределения случайного вектора  задается следующей таблицей:
задается следующей таблицей:
| Y X | ||||||
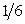 | ||||||
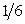 | ||||||
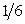 | ||||||
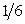 | ||||||
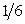 | ||||||
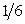 |
Поскольку между случайными величинами X и Y имеется линейная связь 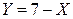 , то
, то 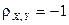 .
.
Ответ: 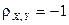 .
.
Теорема. Для любых случайных величин X и Y:
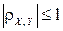 .
.
Определение. Случайные величины X и Y называются некоррелированными, если 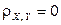 (или
(или 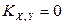 ), иначе X и Y называются коррелированными.
), иначе X и Y называются коррелированными.
Замечание. Из независимости случайных величин следует их некоррелированность. Но из некоррелированности (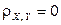 ) не вытекает их независимость. Действительно, если
) не вытекает их независимость. Действительно, если 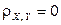 , то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.
, то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.
Пример 2.2.16. Закон распределения случайного вектора  задан таблицей:
задан таблицей:
| Y X | |||
| 0,1 | 0,2 | ||
| 0,3 | |||
| 0,1 | 0,3 |
Выяснить, зависимы или нет случайные величины X и Y. Найти: 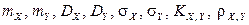 .
.
Решение. Найдем законы распределения компонент X и Y:
| Y X | 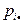 | |||
| 0,1 | 0,2 | 0,3 | ||
| 0,3 | 0,3 | |||
| 0,1 | 0,3 | 0,4 | ||
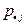 | 0,2 | 0,6 | 0,2 | |
Очевидно, что компоненты X и Y являются зависимыми, т.к.
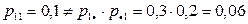 .
.
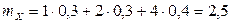 ;
; 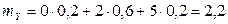 ;
;
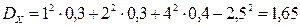 ,
, 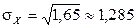 ;
;
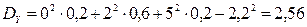 ,
, 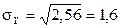 ;
;
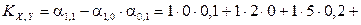
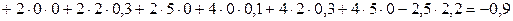 ;
;
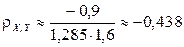 .
.
Так как 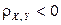 , то это показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет тенденцию уменьшаться.
, то это показывает, что между случайными величинами X и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет тенденцию уменьшаться.
Пример 2.2.17. Закон распределения случайного вектора  задан таблицей:
задан таблицей:
| Y X | ||
| –1 | 0,15 | 0,05 |
| 0,3 | 0,05 | |
| 0,35 | 0,1 |
Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
Решение. Найдем законы распределения компонент X и Y:
| Y X | 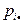 | ||
| –1 | 0,15 | 0,05 | 0,2 |
| 0,3 | 0,05 | 0,35 | |
| 0,35 | 0,1 | 0,45 | |
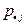 | 0,8 | 0,2 | |
Очевидно, что компоненты X и Y являются зависимыми, т.к.
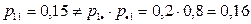 .
.
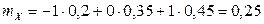 ;
; 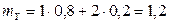 ;
;
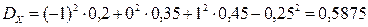 ,
, 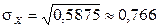 ;
;
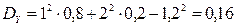 ,
, 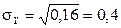 ;
;
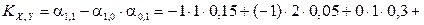
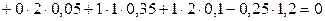 ;
; 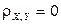 .
.
Этот пример показывает, что случайные величины X и Y могут быть некоррелированными, но при этом являться зависимыми.
Пример 2.2.18. Двумерный случайный вектор  подчинен закону распределения с плотностью
подчинен закону распределения с плотностью
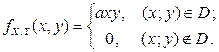
Область D – треугольник, ограниченный прямыми 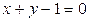 ,
, 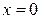 ,
, 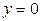 .
.
Найти: коэффициент а, 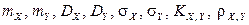 . Выяснить, зависимы или нет случайные величины X и Y.
. Выяснить, зависимы или нет случайные величины X и Y.
Решение. Коэффициент a находится из уравнения
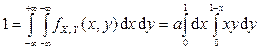 .
.
Опуская промежуточные выкладки (в этом примере будем делать так и в дальнейшем), получаем 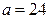 . Далее:
. Далее:
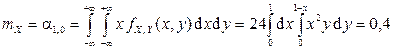 ,
,
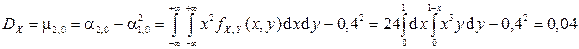 .
.
Заметим, что в силу симметрии по переменным x и y, можно не вычислять математическое ожидание и дисперсию компоненты Y, т.е. 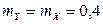 ,
, 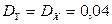 . Тогда
. Тогда 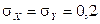 .
.
Вычислим ковариацию и коэффициент корреляции:
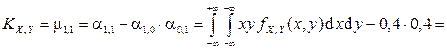
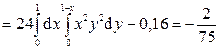 ;
; 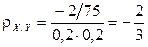 .
.
Поскольку компоненты X и Y коррелированны, следовательно, они зависимы.
 Ответ:
Ответ: 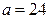 ,
, 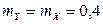 ,
, 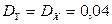 ,
, 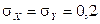 ,
, 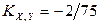 ,
, 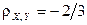 . Компоненты X и Y зависимы.
. Компоненты X и Y зависимы.
Пример 2.2.19. Двумерный случайный вектор  равномерно распределен на множестве случайных точек Q, задаваемых неравенством
равномерно распределен на множестве случайных точек Q, задаваемых неравенством 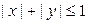 . Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
. Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
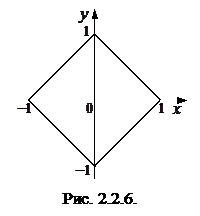
Решение. Множество точек Q, задаваемых неравенством 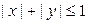 , является квадратом (рис. 2.2.6). Поскольку двумерный случайный вектор
, является квадратом (рис. 2.2.6). Поскольку двумерный случайный вектор  равномерно распределен на множестве Q, его плотность имеет вид
равномерно распределен на множестве Q, его плотность имеет вид
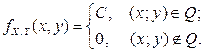
Из условия нормировки найдем константу C:
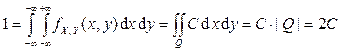 ,
,
где 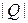 – площадь квадрата Q, равная 2. Отсюда
– площадь квадрата Q, равная 2. Отсюда 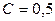 , а значит,
, а значит,
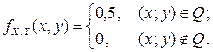
1) Найдем вначале плотность распределения компоненты X.
Если 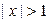 , то, очевидно,
, то, очевидно, 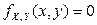 для всех
для всех 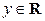 .
.
Если 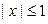 , то
, то
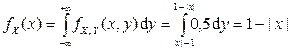 , т.е.
, т.е. 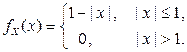
 Аналогично находится плотность распределения компоненты Y:
Аналогично находится плотность распределения компоненты Y:
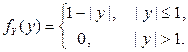
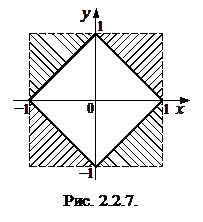
Равенство 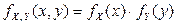 не выполняется для точек координатной плоскости, принадлежащих заштрихованным областям (рис. 2.2.7), поскольку в этих точках
не выполняется для точек координатной плоскости, принадлежащих заштрихованным областям (рис. 2.2.7), поскольку в этих точках 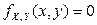 , а
, а 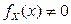 и
и 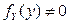 . Суммарная площадь заштрихованных областей равна 2, значит, компоненты X и Y зависимы.
. Суммарная площадь заштрихованных областей равна 2, значит, компоненты X и Y зависимы.
2) Вычислим математические ожидания компонент X и Y:
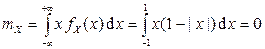 ,
,
т.к. интеграл от нечетной функции в симметричных пределах равен нулю. Аналогично 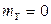 .
.
Определим начальный момент 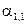 :
:
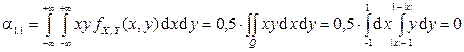 .
.
Таким образом, ковариация 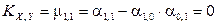 . Значит, компоненты X и Y некоррелированные.
. Значит, компоненты X и Y некоррелированные.
Ответ: компоненты X и Y зависимы, но некоррелированны.
 2015-06-28
2015-06-28 4130
4130
