На практике часто встречаются двумерные случайные величины, распределение которых нормально.
Определение. Нормальным законом распределения на плоскости называется распределение вероятностей двумерной случайной величины  , функция плотности которой имеет вид
, функция плотности которой имеет вид
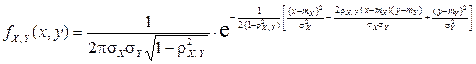 .
.
Итак, нормальный закон на плоскости определяется пятью параметрами: 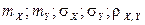 . Смысл этих параметров: математические ожидания и средние квадратические отклонения компонент, а также коэффициент корреляции.
. Смысл этих параметров: математические ожидания и средние квадратические отклонения компонент, а также коэффициент корреляции.
Пример 2.2.26. Доказать, что для нормально распределенных компонент двумерной случайной величины  понятия независимости и некоррелированности равносильны.
понятия независимости и некоррелированности равносильны.
Решение. Действительно, пусть компоненты X и Y некоррелированны (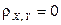 ), тогда плотность
), тогда плотность 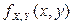 принимает вид:
принимает вид:
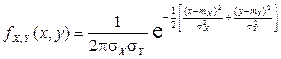 .
.
Отсюда очевидно, что
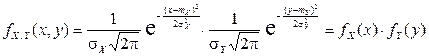 .
.
Значит, компоненты X и Y независимы.
Обратное утверждение также выполняется (из независимости компонент X и Y всегда следует их некоррелированность).
Условные законы распределения случайных величин X и Y:
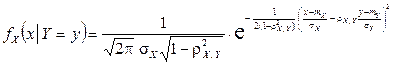 ,
,
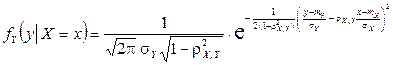 .
.
Нетрудно видеть, что каждый из условных законов распределения также является нормальным с условным математическим ожиданием и условной дисперсией, вычисляемыми по формулам:
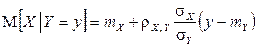 ,
, 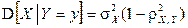 ;
;
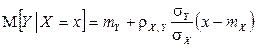 ,
, 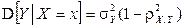 .
.
 Замечание. Из формул для условных математических ожиданий видно, что для системы нормально распределенных случайных величин X и Y линии регрессии Y на x и X на y представляют собой прямые линии, т.е. в данном случае регрессия всегда линейна.
Замечание. Из формул для условных математических ожиданий видно, что для системы нормально распределенных случайных величин X и Y линии регрессии Y на x и X на y представляют собой прямые линии, т.е. в данном случае регрессия всегда линейна.
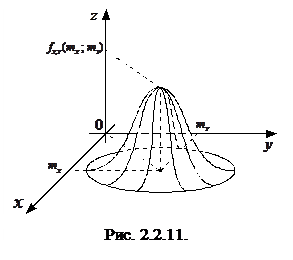
В геометрической интерпретации график 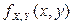 двумерного нормального распределения представляет собой холмообразную поверхность, вершина которой находится в точке
двумерного нормального распределения представляет собой холмообразную поверхность, вершина которой находится в точке 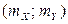 . Аппликата этой вершины равна
. Аппликата этой вершины равна 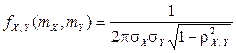 (рис. 2.2.11). Сечения поверхности
(рис. 2.2.11). Сечения поверхности 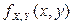 плоскостями, параллельными плоскости xOy, представляют собой эллипсы.
плоскостями, параллельными плоскости xOy, представляют собой эллипсы.
Определение. Нормальное распределение называется круговым с центром в точке 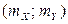 , если случайные величины X и Y некоррелированны (
, если случайные величины X и Y некоррелированны (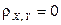 ) и
) и 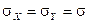 .
.
Пример 2.2.27. Случайная точка  на плоскости xOy распределена по двумерному нормальному закону с центром рассеивания
на плоскости xOy распределена по двумерному нормальному закону с центром рассеивания 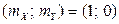 , средними квадратическими отклонениями
, средними квадратическими отклонениями 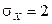 ,
, 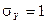 и коэффициентом корреляции
и коэффициентом корреляции 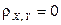 . Вычислить вероятность попадания случайной точки
. Вычислить вероятность попадания случайной точки  в прямоугольник с вершинами
в прямоугольник с вершинами 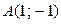 ,
, 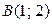 ,
, 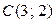 ,
, 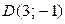 .
.
Решение. Поскольку коэффициент корреляции 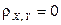 , то плотность
, то плотность 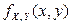 представляется в виде
представляется в виде
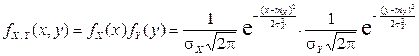 .
.
С учетом того, что 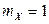 ,
, 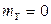 ,
, 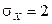 ,
, 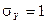 , получим:
, получим:
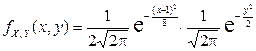 .
.
Поэтому 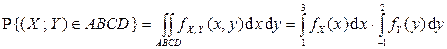 , или
, или
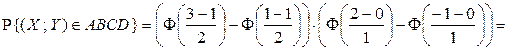
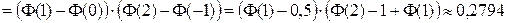 .
.
Ответ: 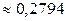 .
.
Пример 2.2.28. Случайные величины X и Y независимы и распределены по нормальному закону. Известно, что 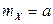 ,
, 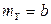 ,
, 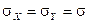 . Найти радиус R круга с центром в точке
. Найти радиус R круга с центром в точке 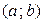 , вероятность попадания в который случайной точки
, вероятность попадания в который случайной точки 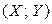 равна 0,997.
равна 0,997.
Решение. Поскольку случайные величины X и Y независимы, то
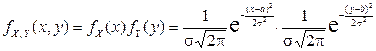 .
.
Вероятность 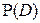 попадания случайной точки
попадания случайной точки 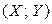 в круг D с центром в точке
в круг D с центром в точке 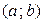 и радиусом R вычисляется следующим образом:
и радиусом R вычисляется следующим образом:
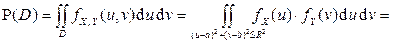
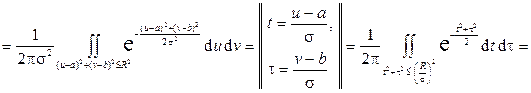
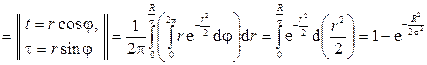 .
.
Теперь, решая уравнение 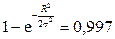 , получим
, получим 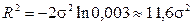 . Отсюда
. Отсюда 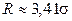 .
.
Ответ: 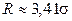 .
.
Пример 2.2.29. Заданы следующие характеристики двумерного нормального вектора 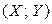 :
: 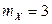 ,
, 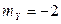 ,
, 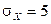 ,
, 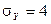 ,
, 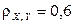 . 1) Записать выражения для плотности распределения вероятностей
. 1) Записать выражения для плотности распределения вероятностей 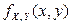 и условных плотностей компонент
и условных плотностей компонент 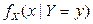 ,
, 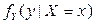 . 2) Составить уравнения регрессий Y на x и X на y. 3) Найти условные дисперсии компонент X и Y.
. 2) Составить уравнения регрессий Y на x и X на y. 3) Найти условные дисперсии компонент X и Y.
Решение. 1) По определению двумерного нормального вектора:
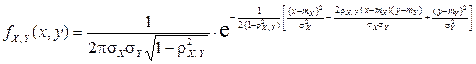 .
.
С учетом того, что 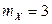 ,
, 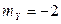 ,
, 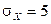 ,
, 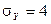 ,
, 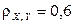 , выражение для
, выражение для 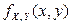 примет вид:
примет вид:
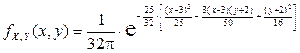 .
.
Условные законы распределения случайных величин X и Y:
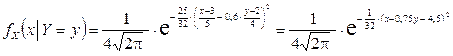 ,
,
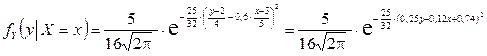 .
.
2) Условные математические ожидания равны:
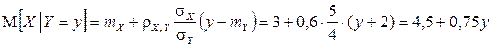 ,
,
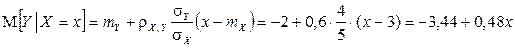 .
.
Таким образом, уравнение регрессии X на y имеет вид 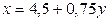 , а уравнение регрессии Y на x имеет вид
, а уравнение регрессии Y на x имеет вид 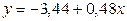 .
.
3) Условные дисперсии равны:
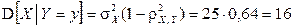 ,
,
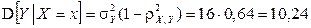 .
.
Ответ: 1) 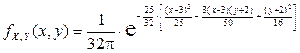 ,
,
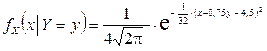 ,
, 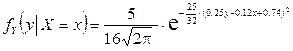 .
.
2) Уравнение регрессии X на y: 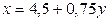 , уравнение регрессии Y на x:
, уравнение регрессии Y на x: 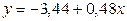 . 3)
. 3) 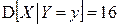 ,
, 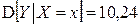 .
.
 2015-06-28
2015-06-28 8570
8570
