Определение. Условным математическим ожиданием одной из случайных величин, входящих в двумерный случайный вектор  , называется ее математическое ожидание, вычисленное при условии, что другая случайная величина приняла определенное значение.
, называется ее математическое ожидание, вычисленное при условии, что другая случайная величина приняла определенное значение.
Если случайные величины X и Y дискретны, то условные математические ожидания вычисляются по формулам:
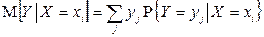 ,
, 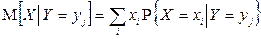 .
.
Если случайные величины X и Y непрерывны, то условные математические ожидания вычисляются по формулам:
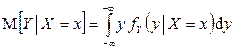 ,
,  .
.
Определение. Условное математическое ожидание случайной величины Y при заданном значении 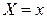 , т.е.
, т.е.  , называется регрессией Y на x. Условное математическое ожидание случайной величины X при заданном значении
, называется регрессией Y на x. Условное математическое ожидание случайной величины X при заданном значении 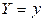 , т.е.
, т.е. 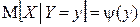 , называется регрессией X на y.
, называется регрессией X на y.
Графики этих зависимостей от x и y называются линиями регрессии Y на x (рис. 2.2.8 а) и X на y (рис. 2.2.8 б) соответственно.
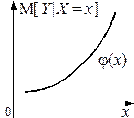
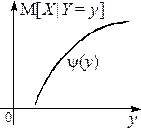
а б
Рис. 2.2.8.
Пример 2.2.24. Закон распределения случайного вектора  задан таблицей:
задан таблицей:
| Y X | |||
| 0,1 | 0,2 | ||
| 0,3 | |||
| 0,1 | 0,3 |
Построить регрессии Y на x и X на y.
Решение. Найдем законы распределения компонент X и Y:
|
|
|
| Y X |  | |||
| 0,1 | 0,2 | 0,3 | ||
| 0,3 | 0,3 | |||
| 0,1 | 0,3 | 0,4 | ||
 | 0,2 | 0,6 | 0,2 | |
Построим вначале регрессию Y на x.
1) 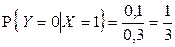 ,
, 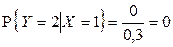 ,
, 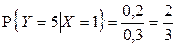 , отсюда
, отсюда 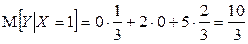 .
.
2) 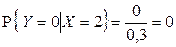 ,
, 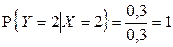 ,
, 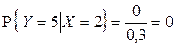 , отсюда
, отсюда 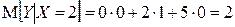 .
.
 3)
3) 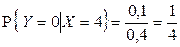 ,
, 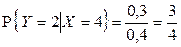 ,
, 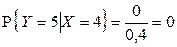 , отсюда
, отсюда 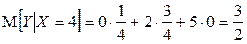 .
.
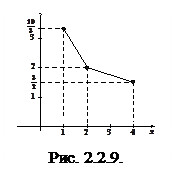
Графическое изображение регрессии Y на x показано на рис. 2.2.9.
Построим теперь регрессию X на y.
1) 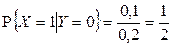 ,
, 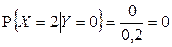 ,
, 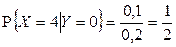 , отсюда
, отсюда 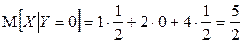 .
.
2) 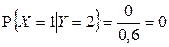 ,
, 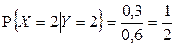 ,
, 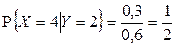 , отсюда
, отсюда 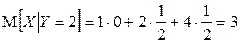 .
.
 3)
3) 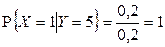 ,
, 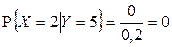 ,
, 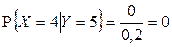 , отсюда
, отсюда 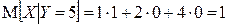 .
.
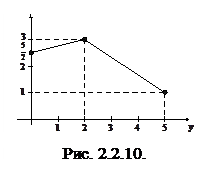
Графическое изображение регрессии X на y показано на рис. 2.2.10.
Для наглядности значения условного математического ожидания на рис. 2.2.9 и 2.2.10 соединены отрезками прямых.
Замечание 1. Для независимых случайных величин линии регрессии Y на x и X на y параллельны координатным осям, т.к. математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина. Линии регрессии могут быть параллельны координатным осям и для зависимых случайных величин, если только математическое ожидание каждой из них не зависит от того, какое значение приняла другая случайная величина.
Замечание 2. По аналогии с условными математическими ожиданиями можно рассматривать условные моменты. Например, условные дисперсии 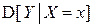 ,
, 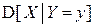 и т.д.
и т.д.
Пример 2.2.25. В примере 2.2.10 была дана функция плотности 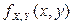 :
:
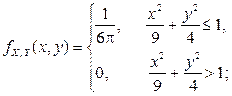
и найдены условные плотности распределения компонент X и Y (пример 2.2.21):
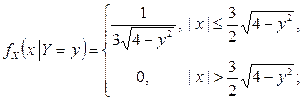
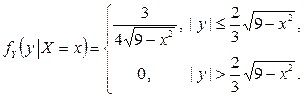
Найти регрессии Y на x и X на y, а также условные дисперсии компонент X и Y.
Решение. Условные математические ожидания вычисляются по формулам:  ,
, 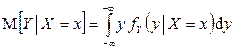 . Поэтому
. Поэтому
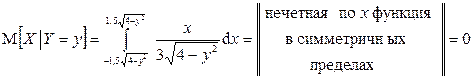 ,
,
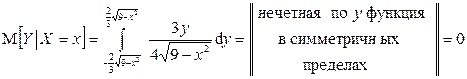 .
.
Заметим, что при вычислении условных математических ожиданий можно было воспользоваться тем, что случайная величина X при условии 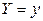 равномерно распределена на отрезке
равномерно распределена на отрезке 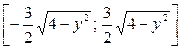 , а случайная величина Y при условии
, а случайная величина Y при условии 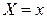 равномерно распределена на отрезке
равномерно распределена на отрезке 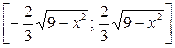 .
.
|
|
|
Действительно, для равномерно распределенной на отрезке 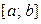 случайной величины математическое ожидание равно
случайной величины математическое ожидание равно 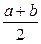 , а дисперсия равна
, а дисперсия равна 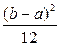 . Отсюда, очевидно,
. Отсюда, очевидно, 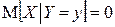 при
при 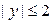 ,
, 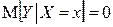 при
при 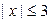 . Тогда условные дисперсии равны:
. Тогда условные дисперсии равны:
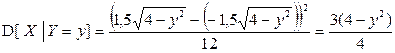 при
при 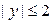 ,
,
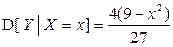 при
при 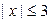 .
.
Ответ: 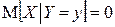 ,
, 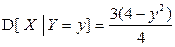 при
при 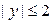 ;
;
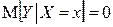 ,
, 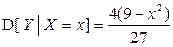 при
при 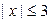 .
.
 2015-06-28
2015-06-28 2048
2048
