2015-06-28
951
2.2.23. Закон распределения случайного вектора 
задан таблицей:
| Y X | |||
| 0,4 | 0,15 | 0,3 | 0,35 |
| 0,8 | 0,05 | 0,12 | 0,03 |
Описать условные законы распределения и найти условные математические ожидания: 1) случайной величины Y при условии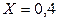 
: 2) случайной величины X при условии 
.
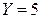2.2.24. Известна плотность совместного распределения непрерывной двумерной случайной величины :
.
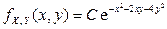Найти: 1) константу C; 2) плотности распределения компонент X и Y; 3) условные плотности распределения компонент X и Y.
2.2.25. Известна плотность совместного распределения непрерывной двумерной случайной величины :
.
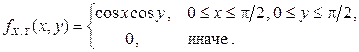Доказать независимость компонент X и Y, найдя плотности и условные плотности их распределения.
2.2.26. Двумерный случайный вектор распределен равномерно внутри трапеции с вершинами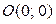 
, 
, 
, 
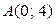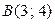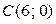. Найти: 1) плотность распределения случайного вектора ; 2) плотности распределения компонент X и Y; 3) условные плотности распределения компонент X и Y.
2.2.27. Случайная точка на плоскости xOy распределена по двумерному нормальному закону с центром рассеивания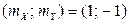 
, средними квадратическими отклонениями 
, 
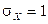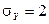и коэффициентом корреляции 
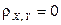. Вычислить вероятность попадания случайной точки в прямоугольник с вершинами ,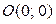 
, 
, 
.
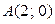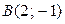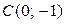2.2.28. На станке-автомате изготавливается деталь цилиндрической формы. Полученные в результате обработки длина L и радиус R детали являются независимыми случайными величинами, распределенными по нормальным законам с характеристиками: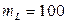 
мм, 
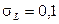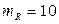мм, 
мм,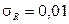 
мм. Установить процент бракованных деталей, если деталь считается годной, когда ее размеры определяются условиями:
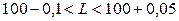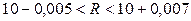мм, 
мм.
2.2.29. Производится стрельба по точечной (малоразмерной) цели, зона поражения которой представляет собой круг радиуса R с центром в начале координат. Рассеивание точки попадания снаряда – нормальное круговое с параметрами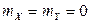 
, 
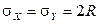. Сколько выстрелов надо произвести, чтобы поразить цель с вероятностью, не мéньшей 0,95?
