Використовуючи критерії видовженості, визначають форму ходу, якщо виконується співвідношення:
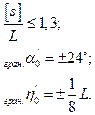
Тут 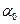 - відхилення напрямку сторони ходу від напрямку замикаючої
- відхилення напрямку сторони ходу від напрямку замикаючої 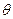
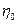 - відстань від вершини ходу до замикаючої.
- відстань від вершини ходу до замикаючої.
Причому граничного значення вказаного в (3.2) може досягнути лише одна із відстаней 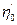 , як рівно один із кутів
, як рівно один із кутів 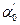 .
.
Для перевірки виконання відношення (3.2) у запроектованому ході проводять замикаючу ходу, відкладають в обидві сторони від неї (в масштабі карти) відстань 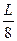 і проводять лінії паралельні до замикаючої.(рис.1.), Якщо жодна із вершин не виходить за межі отриманої смуги, відповідно умову
і проводять лінії паралельні до замикаючої.(рис.1.), Якщо жодна із вершин не виходить за межі отриманої смуги, відповідно умову 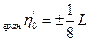 виконано. Величину
виконано. Величину 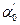 також вимірюють на схемі і порівнюють з граничним значенням вказаним в) (3.2). Хід,
також вимірюють на схемі і порівнюють з граничним значенням вказаним в) (3.2). Хід,
відображений на рис.1, є видовженим, так як 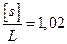 і величини
і величини 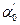 і
і 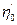 , як видно із креслення, менші за граничні значення.
, як видно із креслення, менші за граничні значення.
3.2. Визначення граничної помилки положення точки в слабому місті ходу після його врівноваження.
Середня квадратична помилка (с.к.п) положення пункту в слабому місці ходу m
(після зрівноваження – це середина ходу) приблизно в 2 рази меньше середньої квадратичної помилки (с.к.п.) кінцевої точки ходу до його зрівнювання. M
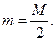 (3.3)
(3.3)
Тоді гранична похибка середньої вершини ходу 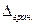 буде рівна 2 m (згідно із допусками) або з врахуванням (3.3) M,
буде рівна 2 m (згідно із допусками) або з врахуванням (3.3) M,
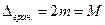 (3.4)
(3.4)
Відповідно, для визначення 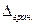 необхідно отримати M. Середня квадратична помилка (с.к.п) положення кінцевої точки ходу M визначається із виразу
необхідно отримати M. Середня квадратична помилка (с.к.п) положення кінцевої точки ходу M визначається із виразу
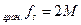 (3.5)
(3.5)
Для якого 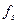 - гранична лінійна помилкаходу – знаходиться із відношення
- гранична лінійна помилкаходу – знаходиться із відношення
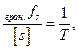 (3.6)
(3.6)
Де 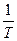 - гранична відносна помилка полігонометричного ходу, яка встановлена Інструкцією[14] для відповідного класу або розряду.
- гранична відносна помилка полігонометричного ходу, яка встановлена Інструкцією[14] для відповідного класу або розряду.
Приклад 1. Визначити середню квадратичну і граничну помилки положення пункта в слабому місті запроектованого зігнутого полігонометричного ходу 4 класу довжиною 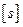 = 6925 м.
= 6925 м.
Розрахунок. Із формул (3.6)і (3.5) знаходимо
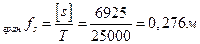
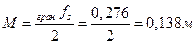
Використовуючи формули (3.3)та (3.4), знаходимо m = 0,069 м; 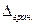 = 0,138 м.
= 0,138 м.
 2015-06-28
2015-06-28 434
434








