2015-06-28
1592
Бинарное отношение называется предпорядком на 
, если оно рефлексивно и транзитивно. Рефлексивное, транзитивное и антисимметричное отношение на множестве называется частичным порядком на . Частичный порядок часто обозначается символом £.
Будем писать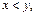 
если х £ у и 
¹ у. Частичный порядок £ на множестве называется линейным, если для любых элементов и у из или £ у или у £ . Множество с заданным на нем частичным порядком (линейным) называется частично (линейно) упорядоченным. Примерами бесконечных линейно упорядоченных множеств являются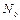 
, Q, R относительно "естественного порядка". Важно заметить, что одно и то же множество можно упорядочить различными способами. Например, натуральные числа можно упорядочить "естественным образом", а можно упорядочить по возрастанию отдельно все нечетные числа и отдельно все четные, считая нечетное число предшествующим всякому четному.
Примером частично, но не линейно упорядоченного множества может служить множество всех пар натуральных чисел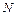 
2 со следующим порядком: (< 
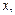у > £ < 
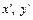>) Û ( £ 
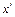, у £ 
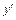). Примером частично упорядоченного множества является множество всех подмножеств данного множества X, упорядоченное по включению 
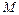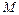£ ¢, если 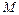Í 
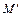, где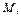 
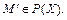
Элемент a частично упорядоченного множества называется максимальным, если а £ Û a = , и минимальным, если £ a Û a =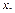 
Элемент a из называется наибольшим элементом, если " х Î : £ а, и наименьшим, если " Î : а £ . Всякий наибольший элемент является максимальным, а всякий наименьший элемент – минимальным. Обратное, вообще говоря, места не имеет. Например, в тривиальном частично упорядоченном множестве (т.е. в котором a £ b Û a = b) всякий элемент является как максимальным, так и минимальным, но не наибольшим и, соответственно, не наименьшим. Верхней (нижней) гранью подмножества 
частично упорядоченного множества называется любой элемент a из такой, что b £ a (a £ b) для любого b Î . Точной верхней (нижней) гранью подмножества Í называется наименьшая верхняя (наибольшая нижняя) грань . Точная верхняя грань множества обозначается 
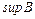(супремум), а точная нижняя грань – 
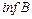(инфимум). Линейный порядок на множестве называется полным, если каждое непустое подмножество множества имеет наименьший элемент. В этом случае множество называется вполне упорядоченным.
Пусть и – частично упорядоченные множества и f – функция из в . Если " x 1, x 2Î : x 1£ x 2 => f (x 1) £ f (x 2), то функция называется монотонной. Если f – взаимно однозначное соответствие между и и f и f –1 монотонны, то f называется изоморфизмом частично упорядоченных множеств и , а множества и называются изоморфными.
