Операции над множествами. Некоторые сведения из теории множеств

Некоторые сведения из теории множеств

Основные понятия

В математике первичными понятиями являются понятия множества и элемента множества. Множества обозначают большими латинскими буквами A, B,…, а их элементы малыми a, b,… Если элемент a принадлежит множеству A, то пишут a ∈ A или A ∍ a. В противном случае пишут a ∉ A. Если элементы a 1, a 2,…, an принадлежат множеству A, то записывают a 1, a 2,…, an ∈ A.

Определение 1.1.

Множество A называется подмножеством множества B, если любой элемент множества A является элементом множества B. Пишут A⊂B или B⊃A и говорят, что множество A включено в множество B или B включает A.

Определение 1.2.

Множества A и B называются равными, если они состоят из одних и тех же элементов. Записывают A=B.

Если множество A включено в множество B или совпадает с ним, то пишут A ⊆ B или B ⊇ A.

Если множество A состоит из элементов a 1, a 2,…, an, то пишут A ={ a 1, a 2,…, an }. Если множество A состоит из элементов, обладающих определённым свойством, то пишут A ={ a:…}, где в фигурных скобках после двоеточия записывают указанное свойство. Например, запись A ={ a: a^ 2−1>0} означает, что множество A состоит из элементов a таких, что a^ 2−1>0.

Определение 1.3.

Множество называется конечным, если оно содержит конечное число элементов. Например, конечно множество дней недели.

Определение 1.4.

Множество, не являющееся конечным, называется бесконечным. Примером бесконечного множества может служить множество всех целых положительных чисел.

Определение 1.5.

Множество, не содержащее ни одного элемента, называется пустым и обозначается ∅

Операции над множествами

Определение 1.6.

Множество C, состоящее из всех элементов двух множеств A и B, называется объединением множеств A и B и обозначается C=A∪B.

Определение 1.7.

Множество C, состоящее из всех элементов, одновременно принадлежащих как множеству A, так и множеству B, называется пересечением множеств A и B и обозначается C=A∩B.

Определение 1.8.

Множество C, состоящее из всех элементов множества A, не принадлежащих множеству B, называется разностью множеств A и B и обозначается C=A\B.

Определение 1.9.

Если множество B является подмножеством множества A, то множество A\B называется дополнением B до A.

На рис 1.1 дана графическая иллюстрация введенных операций над множествами A и B. Заштрихованная часть плоскости соответствует объединению (рис. 1.1, а), пересечению (рис. 1.1, б), разности (рис. 1.1, в) множеств A и B и дополнению множества B до A (рис. 1.1, г).

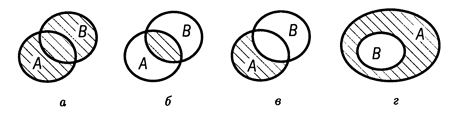
Рис. 1.1

Пусть, например, A ={1,2,3,4,5}, B ={2,4,6,8}. Тогда A ∪ B ={1,2,3,4,5,6,8}, A ∩ B ={2,4}, A \ B ={1,3,5}. Дополнение множества B до множества A не определено, так как множество B не является подмножеством множества A.