А. Скалярное произведение векторов

Определение 20. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается скалярное произведение символом 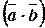или .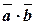

Скалярное произведение векторов можно выразить формулами:

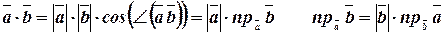
Отсюда скалярное произведение двух векторов равно произведению длины одного вектора на проекцию на него другого.

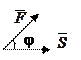Пусть вектор перемещения 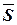будет неподвижен, а точка приложения вектора силы 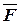скользит вдоль вектора 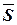, тогда

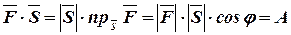
есть работа, совершаемая под действием силы 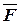вдоль вектора .

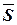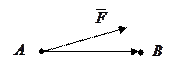Пример 3. Вычислить, какую работу производит сила 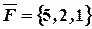, когда точка ее приложения перемещается из 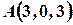в .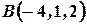

Решение. Образуем вектор перемещения .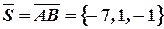

Тогда работа .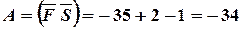

Скалярное произведение векторов, заданных своими координатами.

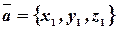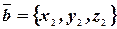Пусть и тогда

.

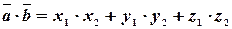Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат.