Указание. Все последующие расчеты и графические построения выполняются для нешунтированного и шунтированного контура при полном и частичном подключении (ЧП). Результаты (кроме п.10) заносятся в табл. 5.2.
1. Рассчитайте резонансную частоту 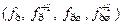 и коэффициент подключения (p) контура.
и коэффициент подключения (p) контура.
2. Рассчитайте характеристическое сопротивление 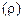 , а также эквивалентные сопротивления вносимые в контур при шунтировании полного и ЧП контуров
, а также эквивалентные сопротивления вносимые в контур при шунтировании полного и ЧП контуров 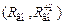 .
.
3. Рассчитайте добротность 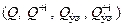 и полосу пропускания
и полосу пропускания 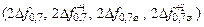 контура.
контура.
4. Рассчитайте и постройте нормированные резонансные кривые 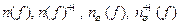 контура. Пометьте на каждой кривой полосу пропускания.
контура. Пометьте на каждой кривой полосу пропускания.
5. Рассчитайте коэффициент затухания 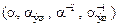 , постоянную времени
, постоянную времени 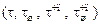 и время установления переходного процесса
и время установления переходного процесса 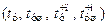 .
.
6. Определите декремент затухания 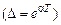 и логарифмический декремент затухания
и логарифмический декремент затухания 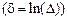 .
.
7. Изобразите качественно вид нормированных переходных характеристик 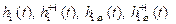 . Пометьте на графиках
. Пометьте на графиках 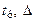 .
.
8. Рассчитайте резонансное сопротивление контура 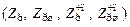 .
.
9. Вычислите действующие значения напряжения на полном (Uвых1) и ЧП (Uвых2) контуре без шунта и с шунтом, если амплитуда входного гармонического тока 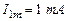 .
.
10. Вычислите действующие значения напряжения на полном (Uвых1) контуре при подключении входного гармонического тока амплитудой 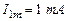 к части контура (без шунта и с шунтом).
к части контура (без шунта и с шунтом).
11. Определите амплитуду прямоугольных импульсов источника тока 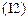 , которые необходимо подать на контур так, чтобы на выходе осциллограф показал нормированную переходную характеристику.
, которые необходимо подать на контур так, чтобы на выходе осциллограф показал нормированную переходную характеристику.
Таблица 5.2.
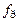 кГц кГц | 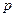 | 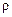 Ом Ом | 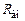 кГц кГц | 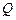 | 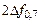 кГц кГц | 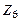 кОм кОм | 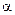 | 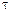 мс мс | 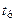 мс мс | 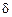 | 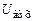 В В | 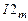 мА мА | |
| Полный контур (ПК) | |||||||||||||
| ПК с шунтом | |||||||||||||
| Частично подключенный (ЧП) контур | |||||||||||||
| ЧП контур с шунтом |
Расчетные соотношения [4, 5]
Резонансная частота 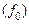 , характеристическое сопротивление
, характеристическое сопротивление 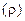 , эквивалентное сопротивление потерь
, эквивалентное сопротивление потерь 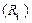 , добротность контура
, добротность контура 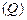 , полоса пропускания (
, полоса пропускания (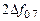 ) и резонансное сопротивление контура без учета сопротивления шунта
) и резонансное сопротивление контура без учета сопротивления шунта 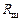 рассчитываются по формулам
рассчитываются по формулам
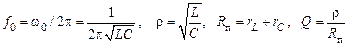 ,
,
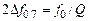 ,
, 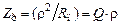 .
.
Нормированная передаточной резонансная характеристика контура
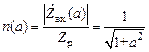 ,
,
где 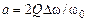 – обобщенная расстройка, в которой можно выделить:
– обобщенная расстройка, в которой можно выделить: 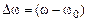 – абсолютную и
– абсолютную и 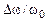 – относительную расстройки.
– относительную расстройки.
Свойства цепи во временной области определяются переходной характеристикой h (t). В нашем случае h (t) представляет собой реакцию контура на единичный скачёк тока. Для контура с малыми потерями (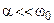 ) нормированная переходная характеристика
) нормированная переходная характеристика
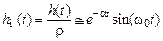 ,
,
где 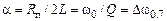 – коэффициент затухания. По уровню 0.05 графика
– коэффициент затухания. По уровню 0.05 графика 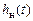 вычисляют время установления свободных колебаний (
вычисляют время установления свободных колебаний (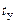 ) и постоянную времени (
) и постоянную времени (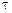 ) контура
) контура
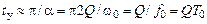 ,
, 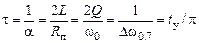 .
.
Логарифмический декремент затухания
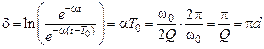 ,
,
где 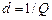 – затухание контура.
– затухание контура.
Подключение параллельно контуру сопротивление шунта уменьшит входное сопротивление контура на резонансной частоте
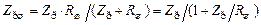 .
.
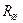 , пересчитанное из параллельной ветви в последовательную, называется вносимым сопротивлением
, пересчитанное из параллельной ветви в последовательную, называется вносимым сопротивлением
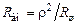 .
.
Появление в контуре дополнительного сопротивления потерь 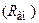 изменит его частотные и временные свойства. Численно изменения можно оценить с помощью эквивалентной добротности и эквивалентного коэффициента затухания
изменит его частотные и временные свойства. Численно изменения можно оценить с помощью эквивалентной добротности и эквивалентного коэффициента затухания
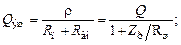
Для ослабления влияния сопротивлений, шунтирующих контур, используют сложные контуры с разделенными реактивными элементами. Их называют контурами с частичным подключением (ЧП). Например, с частичным подключением индуктивности.
При частичном подключении резонансная частота не меняется, а входное сопротивление контура 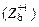 уменьшается
уменьшается
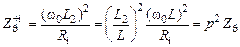 ,
,
где 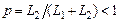 – коэффициент включения;
– коэффициент включения; 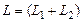 – полная индуктивность.
– полная индуктивность.
Входное сопротивление при шунтировании частично подключенного контура равно
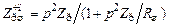 .
.
Амплитуда напряжения на полном 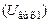 , полном шунтированном
, полном шунтированном 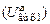 , частично подключённом
, частично подключённом 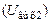 и частично подключённом шунтированном контуре
и частично подключённом шунтированном контуре 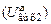 при подключении к нему источника тока с амплитудой
при подключении к нему источника тока с амплитудой 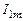
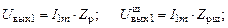
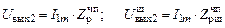 .
.
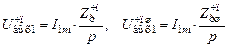 .
.
 2015-06-28
2015-06-28 1086
1086








