2015-06-28
1621
Лабораторная работа № 5
КОЛЕБАТЕЛЬНЫе КОНТУРы
Цель работы
Изучение частотных и переходных характеристик параллельного и последовательного колебательных контуров.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Параллельный контур
 |
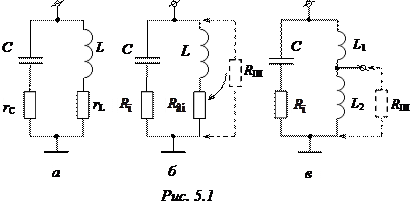Простой параллельный колебательный контур состоит из параллельного соединения катушки индуктивности и конденсатора, которые на схеме (рис. 5.1, а) изображены как индуктивность (L) и ёмкость (C) со своими сопротивлениями потерь (r L и r C).
Резонансная частота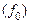 
, характеристическое сопротивление 
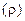, эквивалентное сопротивление потерь 
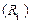и добротность контура 
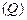рассчитываются по формулам
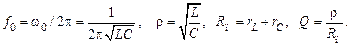(5.1)
Комплексное входное сопротивлением контура определяет его свойства в частотной области.
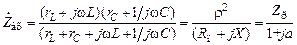, (5.2)
где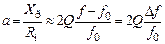 
– обобщенная расстройка;
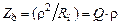– резонансное сопротивление (сопротивление колебательного контура на резонансной частоте).
Нормированной передаточной характеристикой резонансного контура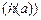 
называется отношение
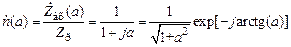. (5.3)
На рис. 5.2 построены АЧХ (
) и ФЧХ (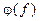
) параллельного контура. Из графика АЧХ следует, что контур можно использовать в качестве полосового фильтра. Нижняя и верхняя граничные частоты 
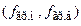полосы пропускания фильтра вычисляются по уровню 
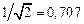АЧХ. Полоса пропускания контура 
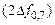зависит от его добротности
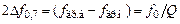. (5.4)
Свойства цепи во временной области определяются переходной характеристикой h (t). В нашем случае h (t) представляет собой реакцию контура на единичный скачёк тока, имеет размерность сопротивления и может быть найдена как обратное преобразование Лапласа от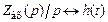 
.
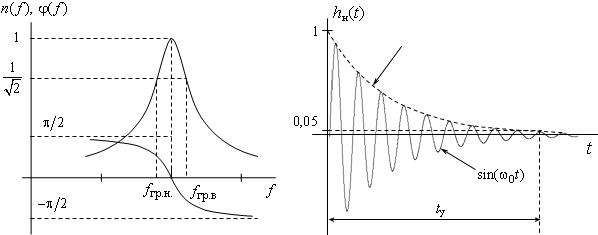
Рис. 5.2. Частотные характеристики Рис.5.3. Переходная характеристика
Для контура с малыми потерями (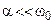
) нормированная переходная характеристика
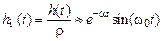. (5.5)
Коэффициент затухания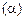 
и постоянная времени контура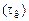 
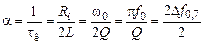. (5.6)
На рис. 5.3 изображен график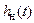 
. Длительность переходного процесса (t у), т.е. время затухания в контуре собственных колебаний, можно определить графически по уровню 0.05 или вычислить по формуле
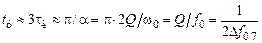. (5.7)
Кроме того, скорость затухания собственных колебаний можно оценить отношением амплитуд переходного процесса через период (декрементом затухания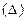 
). Логарифм этого отношения называется логарифмическим декрементом затухания
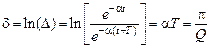. (5.8)
Подключение параллельно контуру сопротивление шунта (рис. 5.3, б) уменьшит входное сопротивление контура на резонансной частоте
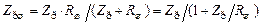. (5.9)
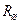, пересчитанное из параллельной ветви в последовательную, (рис. 5.1, б) называется вносимым сопротивлением
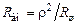, (5.10)
Появление в контуре дополнительного сопротивления потерь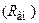 
изменит его частотные и временные свойства. Численно изменения можно оценить с помощью эквивалентной добротности и эквивалентного коэффициента затухания
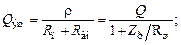(5.11а)
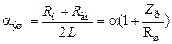. (5.11б)
Для ослабления влияния сопротивлений, шунтирующих контур, используют сложные контуры с разделенными реактивными элементами. Их называют контурами с частичным подключением (ЧП). Например, с частичным подключением индуктивности (рис. 5.1, в).
При частичном подключении резонансная частота не меняется, а входное сопротивление контура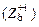 
уменьшается, так как используется только часть реактивного элемента (например, L 2 на рис. 5.1, в)
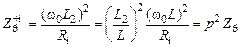, (5.12)
где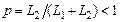 
– коэффициент включения; 
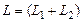– полная индуктивность.
Входное сопротивление при шунтировании частично подключенного контура равно
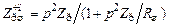. (5.13)
Важно! Вносимое сопротивление потерь при шунтирования только части контура уменьшается в p2 раз
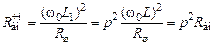, (5.14)
т.е. влияние шунта на свойства контура ослабляется.
Амплитуда напряжения на полном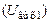 
, полном шунтированном 
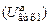, частично подключённом 
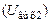и частично подключённом шунтированном контуре 
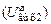при подключении к нему тока амплитудой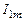 
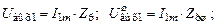(5.15а)
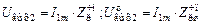. (5.15б)
Важно подчеркнуть. При подключении к источнику тока только части контура выходное напряжение, снимаемое с этой части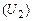 
, изменяется в p2 раз, а снимаемое с полного контура 
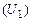- в p раз т.к.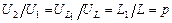 
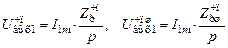(5.16)
