Автоматом называют дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы.
Если множество состояний автомата, а так же множество входных и выходных сигналов конечны, то автомат называют конечным автоматом. Все реальные автоматы являются конечными.
Информацию, поступающую на вход автомата, и преобразующую входную информацию принято кодировать конечной совокупностью символов. Эту совокупность называют алфавитом, отдельные символы, образующие алфавит буквами, а любые конечные упорядоченные последовательности букв данного алфавита словами в этом алфавите.
Автоматы функционируют в дискретные моменты времени, которые обозначаются натуральными числами t=0, 1, 2,…. В каждый момент дискретного времени на вход автомата поступает один сигнал (буква), фиксируется определённое состояние автомата и с выхода снимается один сигнал. Реальные автоматы могут иметь, вообще говоря, несколько входов и выходов. В некоторых случаях для решения задач синтеза удобно заменить такие автоматы автоматами с одним входом и одним выходом. Для этого достаточно закодировать соответствующим образом входные и выходные сигналы исходного алфавита. Если, например, автомат имеет два входа, на каждый из которых подаются сигналы 0 или 1, то все возможные комбинации входных сигналов можно закодировать четырьмя буквами (0, 0), (0, 1), (1, 0), (1, 1).
Процесс дискретного преобразования информации автоматами можно описать с помощью детерминированных функций.
Обозначим через 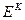 ={0, 1, …, k-1}, где k – некоторое натуральное число, а через
={0, 1, …, k-1}, где k – некоторое натуральное число, а через 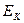 множество всех k-значных последовательностей a таких, что а ={ a (1), a (2),…, a (t), …}, где a (i)
множество всех k-значных последовательностей a таких, что а ={ a (1), a (2),…, a (t), …}, где a (i) 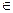
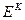 для всех i=1, 2,….
для всех i=1, 2,….
Обозначим через 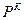 множество всех функций y= f
множество всех функций y= f 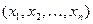 определённых на наборах
определённых на наборах 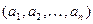 , где
, где 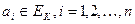 и принимающие значение из
и принимающие значение из 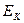 . Функции из
. Функции из 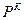 преобразуют наборы k-значных последовательностей в k-значные последовательности. В множество
преобразуют наборы k-значных последовательностей в k-значные последовательности. В множество 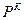 включим так же все последовательности из
включим так же все последовательности из 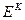 , рассматривая их как функции, зависящие от пустого множества переменных, т. е. как константы.
, рассматривая их как функции, зависящие от пустого множества переменных, т. е. как константы.
С помощью векторной записи функции от n переменных из 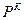 можно свести к функции от одной переменной. Обозначим набор переменных
можно свести к функции от одной переменной. Обозначим набор переменных 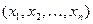 через Х, вместо y= f
через Х, вместо y= f 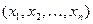 будем писать y= f (Х). При этом значение переменной Х есть вектор а =
будем писать y= f (Х). При этом значение переменной Х есть вектор а = 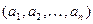 компонентами которого являются последовательности из
компонентами которого являются последовательности из 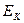 ,
, 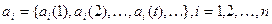 . Будем рассматривать а как последовательность векторов
. Будем рассматривать а как последовательность векторов 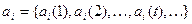 , где
, где 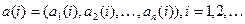 .
.
Таким образом, мы будем считать, что выполняется тождество: 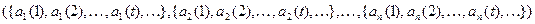 =
= 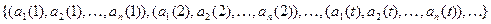 .
.
Лемма 1 Число наборов 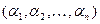 , где
, где 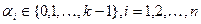 равно
равно 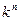 .
.
Итак, функцию y= f 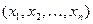
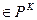 с помощью векторной записи можно свести к функции y=
с помощью векторной записи можно свести к функции y= 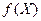
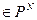 , где N=
, где N= 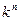 . Таким образом, изучение функции y= f
. Таким образом, изучение функции y= f 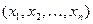 из
из 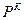 можно свести к изучению функции от одной переменной из
можно свести к изучению функции от одной переменной из 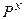 , где N=
, где N= 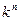 .
.
Определение 1 Функция y= 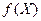 из
из 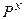 называется детерминированной, если каково бы ни было число t и каковы бы ни были последовательности а и b такие, что a(1)=b(1), a(2)=b(2), … a(t)=b(t) значение функций α, β, где α=
называется детерминированной, если каково бы ни было число t и каковы бы ни были последовательности а и b такие, что a(1)=b(1), a(2)=b(2), … a(t)=b(t) значение функций α, β, где α= 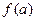 , β=
, β= 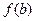 представляют собой последовательности, у которых тоже совпадают первые t членов, т. е.
представляют собой последовательности, у которых тоже совпадают первые t членов, т. е.
α(1)=β(1), α(2)=β(2), …, α(t)=β(t).
Множество всех детерминированных функций обозначим через 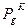 .
.
Из определения детерминированной функции следует, что значение α (t) (α= 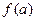 ) зависит только от значения первых t членов входной последовательности а, т. е. а(1), а(2), …, а(t), следовательно α(t)=φ(а(1), а(2), …, а(t)).
) зависит только от значения первых t членов входной последовательности а, т. е. а(1), а(2), …, а(t), следовательно α(t)=φ(а(1), а(2), …, а(t)).
Приведём примеры как детерминированных, так и недетерминированных функций.
Пример 1 Рассмотрим функцию y= 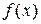
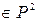 , определённую следующим образом
, определённую следующим образом 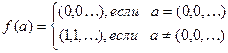
Покажем, что данная функция недетерминированная. Действительно, возьмём две входные последовательности 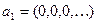 и
и 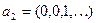 . Тогда
. Тогда 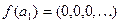 и
и 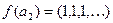 . Следовательно, данная функция недетерминированная.
. Следовательно, данная функция недетерминированная.
Пример 2 Рассмотрим функцию 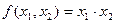 из
из 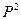 , определённую следующим образом
, определённую следующим образом 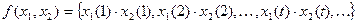 .Здесь выходная последовательность – почленная конъюнкция входных последовательностей. Очевидно, что
.Здесь выходная последовательность – почленная конъюнкция входных последовательностей. Очевидно, что 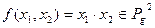 .
.
Пример 3 Рассмотрим функцию z= x +y 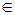
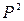 осуществляющую сложение 2-значных последовательностей в двоичной системе с бесконечным числом разрядов. Для этого используется обычный алгоритм сложения двух чисел столбиком
осуществляющую сложение 2-значных последовательностей в двоичной системе с бесконечным числом разрядов. Для этого используется обычный алгоритм сложения двух чисел столбиком
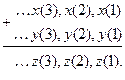
Очевидно, что z(t) определяется по первым t слагаемых, т. е. x +y 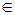
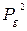 .
.
Детерминированная функция 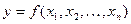 может быть проинтерпретирована следующим образом. Пусть мы имеем некоторый «дискретный преобразователь», в котором существует n входов
может быть проинтерпретирована следующим образом. Пусть мы имеем некоторый «дискретный преобразователь», в котором существует n входов 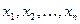 и один выход
и один выход 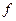 .
.


На входы в моменты времени t = 1,2, …, m, … подаются входные последовательности
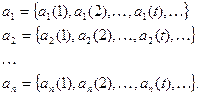
И в эти же моменты t на выходе возникает выходная последовательность 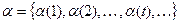 , причем
, причем 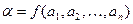 . Очевидно, что в дискретном преобразователе значения α(t) зависит только от значений входных последовательностей в момент времени 1,2, …, t и не зависит от значений в будущие моменты времени. Поэтому преобразование
. Очевидно, что в дискретном преобразователе значения α(t) зависит только от значений входных последовательностей в момент времени 1,2, …, t и не зависит от значений в будущие моменты времени. Поэтому преобразование 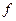 есть детерминированная функция.
есть детерминированная функция.
Пусть 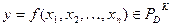 . Выше мы показали, что с помощью векторной записи данную функцию можно свести к функции
. Выше мы показали, что с помощью векторной записи данную функцию можно свести к функции 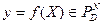 , где
, где 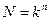 . Рассмотрим бесконечную фигуру:
. Рассмотрим бесконечную фигуру:
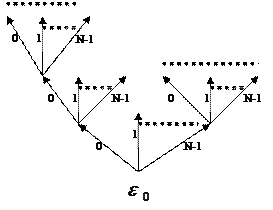
|
Построена она следующим образом, и называть её будем деревом. Возьмём произвольную вершину 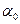 , которую назовём корнем дерева. Из неё проведём N рёбер, которые образуют первый ярус. Из концов каждого из рёбер также проведём N рёбер, которые образуют второй ярус и т. д. Рёбра каждого пучка нумеруются слева направо числами 0,1,…,N-1 или их значениями в k-ичной системе счисления.
, которую назовём корнем дерева. Из неё проведём N рёбер, которые образуют первый ярус. Из концов каждого из рёбер также проведём N рёбер, которые образуют второй ярус и т. д. Рёбра каждого пучка нумеруются слева направо числами 0,1,…,N-1 или их значениями в k-ичной системе счисления.
В дальнейшем на рисунках номера рёбер будут опускаться. Далее, каждому ребру в построенном дереве произвольным образом припишем одно из чисел множества {0,1,…,k-1}. В результате получим так называемое нагруженное дерево. Рассмотрим следующее нагруженное дерево.
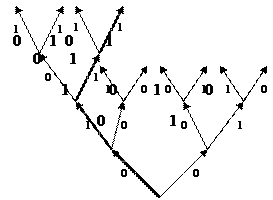

Начиная движение с корня дерева, пойдём по рёбрам. Так, например, последовательности (0,0,1,1…), где числа 0,0,1,1, … - номера рёбер, соответственно, 1-го,2-го,3-го,4-го и т. д. ярусов соответствует выделенный маршрут и последовательность (0,1,1,1…).
Теорема 1 Функция из 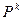 будет детерминированной тогда и только тогда, когда она может быть заданна с помощью нагруженного дерева.
будет детерминированной тогда и только тогда, когда она может быть заданна с помощью нагруженного дерева.
Доказательство Покажем, что любое нагруженное дерево задает некоторую детерминированную функцию. Действительно, пусть 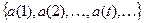 – произвольная последовательность чисел, где
– произвольная последовательность чисел, где 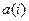
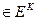 , i=1,2,…. Будем считать, что
, i=1,2,…. Будем считать, что 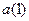 - номер ребра 1-го яруса,
- номер ребра 1-го яруса, 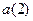 - номер ребра 2-го яруса и т. д. Данной последовательности в нагруженном дереве соответствует единственный маршрут, ведущий из корня дерева. Числа, приписанные выделенным ребрам образуют выходную последовательность
- номер ребра 2-го яруса и т. д. Данной последовательности в нагруженном дереве соответствует единственный маршрут, ведущий из корня дерева. Числа, приписанные выделенным ребрам образуют выходную последовательность 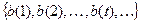 . Покажем, что построенная функция из
. Покажем, что построенная функция из 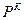 является детерминированной. Пусть
является детерминированной. Пусть 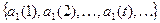 и
и 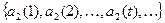 – две входные последовательности такие, что
– две входные последовательности такие, что 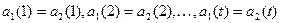 . Ясно, что маршруты в нагруженном дереве, соответствующие данным последовательностям на первых t ярусах совпадают. А это значит, что
. Ясно, что маршруты в нагруженном дереве, соответствующие данным последовательностям на первых t ярусах совпадают. А это значит, что 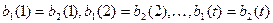 , т. е. функция детерминированная. Обратное утверждение очевидно. Теорема доказана.
, т. е. функция детерминированная. Обратное утверждение очевидно. Теорема доказана.
Рассмотрим следующие примеры:
Пример 4 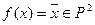 . Ясно, что
. Ясно, что 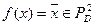 и число ребер, выходящих из вершин равно
и число ребер, выходящих из вершин равно 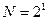 . Построим дерево соответствующее данной функции.
. Построим дерево соответствующее данной функции.
..........
|
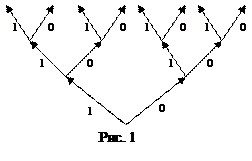

Например, входной последовательности {0,1,1,…} будет соответствовать входная последовательность {1,0,0,…}.
Пример 5 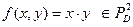 , которая задаётся следующим образом.
, которая задаётся следующим образом.
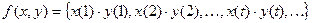 , где x (t)·y(t) – конъюнкция.
, где x (t)·y(t) – конъюнкция.
Для данной функции k=n=2 и число ребер, выходящих из вершин равно N= 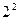 =4. Ребру с номером D=(0,0) соответствует значение (0,0)=0
=4. Ребру с номером D=(0,0) соответствует значение (0,0)=0
1=(0,1) 0·1=0
2=(1,0) 1·0=0
3=(1,1) 1·1=1.
Следовательно, данной функции соответствует следующее нагруженное дерево.
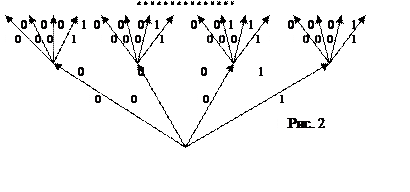

Пример 6 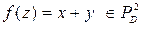 , k=n=1, N=
, k=n=1, N= 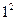 =1.
=1.
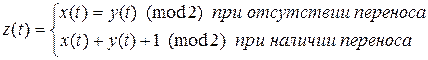
Дерево, соответствующее данной функции строится следующим образом. Процесс приписывания ребрам чисел начинается с 1-го яруса
0=(0,0) 0+0=0
1=(0,1) 0+1=1
2=(1,0) 1+0=1
3=(1,1) 1+1=0
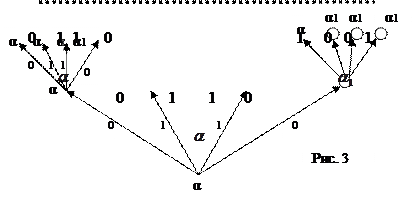
При этом, если появляется перенос в следующий разряд, то конец соответствующего ребра кончается кружочком. Это позволяет выполнить вычисление в следующем ярусе.

Возьмем нагруженное дерево для некоторой детерминированной функции 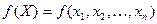 . Пусть
. Пусть 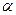 - произвольная его вершина
- произвольная его вершина 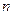 -го яруса. Данную вершину можно рассматривать как корень нагруженного дерева. Согласно теореме 1 оно определяет некоторую детерминированную функцию
-го яруса. Данную вершину можно рассматривать как корень нагруженного дерева. Согласно теореме 1 оно определяет некоторую детерминированную функцию 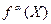 .
.
Определение 2 Два поддерева с корнями 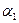 и
и 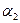 исходного дерева называются эквивалентными, если
исходного дерева называются эквивалентными, если 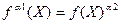 .
.
Очевидно, что при естественном наложении двух эквивалентных поддеревьев их нумерации совпадают. Так, в дереве Рис.1 и Рис.2 все поддеревья эквивалентны, а в дереве (Рис.3) поддеревья с корнями 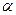 эквивалентны, а с корнями
эквивалентны, а с корнями 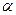 и
и 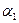 не эквивалентны.
не эквивалентны.
Определение 3 Весом дерева и весом соответствующей детерминированной функции называется максимальное число попарно неэквивалентных поддеревьев.
Например, все функции из примеров 4,5 равен 1, а из примера 6 равен 2.
Определение 4 Детерминированная функция 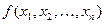 называется ограниченно – детерминированной функцией, если она имеет конечный вес.
называется ограниченно – детерминированной функцией, если она имеет конечный вес.
Класс всех ограниченно – детерминированных функций обозначим через 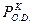
Функции из примеров 4,5,6 являются ограниченно-детерминирован ны-
ми функциями.
Рассмотрим следующую детерминированную функцию.
Пример 7 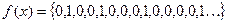
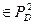 . Ясно, что вес данной функции
. Ясно, что вес данной функции 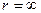 , т. е. она не является ограниченно-детерминированной.
, т. е. она не является ограниченно-детерминированной.
Пусть 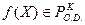 , вес которой равен r. Рассмотрим алфавит
, вес которой равен r. Рассмотрим алфавит 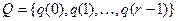 , который назовём внутренним алфавитом. Каждой вершине нагруженного дерева, соответствующей функции
, который назовём внутренним алфавитом. Каждой вершине нагруженного дерева, соответствующей функции 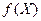 припишем одну из букв алфавита
припишем одну из букв алфавита 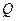 с соблюдением следующего правила: эквивалентным вершинам приписываются одни и те же буквы из
с соблюдением следующего правила: эквивалентным вершинам приписываются одни и те же буквы из 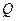 . В результате получаем так называемое полное нагруженное дерево.
. В результате получаем так называемое полное нагруженное дерево.
Для любой ограниченно – детерминированной функции соответствующее ей полное нагруженное дерево можно свести к коечному дереву с занумерованными ребрами и вершинами. Если в нем провести отождествление эквивалентных вершин, то получим так называемую диаграмму Мура. В ней нулём отмечена начальная вершина и ребрам приписаны пары чисел (a, b), первое из которых обозначает номер ребра, а второе число соответствующее этому ребру. Так функция 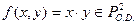 соответствует диаграмме Мура.
соответствует диаграмме Мура.
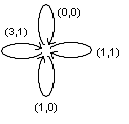
А функция 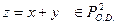
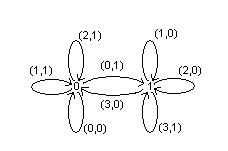
Пусть 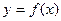 - ограниченно-детерминированная функция с весом r.
- ограниченно-детерминированная функция с весом r.
Пусть 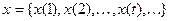 - входная последовательность. Ей соответствует выходная последовательность
- входная последовательность. Ей соответствует выходная последовательность 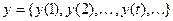 и последовательность состояний
и последовательность состояний 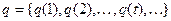 .
.
Возьмем другую входную последовательность 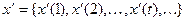 .
.
Ей соответствуют, соответственно, выходная последовательность и последовательность состояний
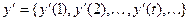
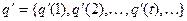 .
.
В общем случае из того, что 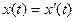 не следует, что
не следует, что 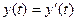 . Однако, если
. Однако, если 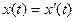 и
и 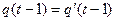 , то
, то 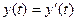 и
и 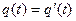 . Другими словами это означает, что если два одноименных ребра (
. Другими словами это означает, что если два одноименных ребра (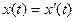 ) выходят из эквивалентных вершин (
) выходят из эквивалентных вершин (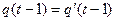 ), то они будут нагружены одной и той же буквой (
), то они будут нагружены одной и той же буквой (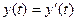 ) и входить в эквивалентные вершины (
) и входить в эквивалентные вершины (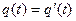 ). Это означает, что
). Это означает, что
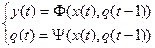 (*)
(*)
Уравнения (*) называются каноническими уравнениями функции 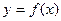 . Первое уравнение называется уравнением выход, второе уравнением перехода.
. Первое уравнение называется уравнением выход, второе уравнением перехода.
Уравнение (*) можно задать с помощью канонической таблицы.
| x (t) | q(t-1) | y(t) | q(t) |
Пусть x (t) и y(t) из {0,1}, а 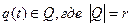 . Если вес r≤2, то каноническая таблица есть таблица истинности. Если r>2, то каноническая таблица не является таблицей истинности. Но с помощью кодирования всех чисел алфавита
. Если вес r≤2, то каноническая таблица есть таблица истинности. Если r>2, то каноническая таблица не является таблицей истинности. Но с помощью кодирования всех чисел алфавита 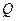 в двоичной системе счисления мы её можем преобразовать в таблицу истинности.
в двоичной системе счисления мы её можем преобразовать в таблицу истинности.
Рассмотрим теперь функцию от n переменных 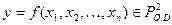 с весом r>1,
с весом r>1, 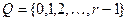 - внутренний алфавит. Закодируем все числа из алфавита
- внутренний алфавит. Закодируем все числа из алфавита 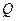 в двоичной системе счисления наборами из {0,1} длинной
в двоичной системе счисления наборами из {0,1} длинной 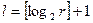 . В этом случае канонические уравнения искомой функции имеют вид.
. В этом случае канонические уравнения искомой функции имеют вид.
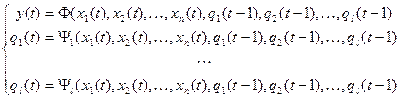 (**)
(**)
В дальнейшем договоримся, что начальные состояния в канонических уравнениях (**) q (0)=0, а в уравнениях (*) 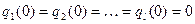 .
.
Пример 8 Найти канонические уравнения функции 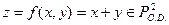
Ранее мы показали, что вес данных функций равен 2 и её диаграмма Мура
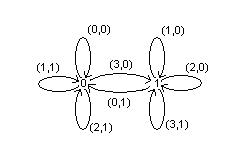
Построим каноническую таблицу.
| x (t) | y(t) | q(t-1) | z(t) | q(t) |
Данная каноническая таблица является таблицей истинности.
Запишем канонические уравнения, используя результаты раздела 3.
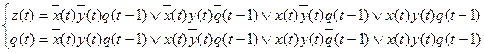
Используя законы алгебры логики
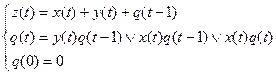
Пример 9 Найти каноническое уравнение для функции заданной следующей диаграммой Мура
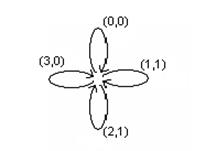
Строим каноническую таблицу.
| x (t) | y(t) | q(t-1) | z(t) | q(t) |
Отсюда 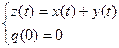
Заметим, что если вес функции равен 1, то в канонических уравнениях 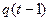 будет отсутствовать.
будет отсутствовать.
Пример 10 Найти канонические уравнения ограниченно-детерминиро-
ванной функции заданной следующей диаграммой Мура:
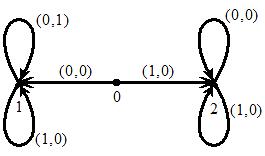
Ясно, что вес данной функции равен 3. Построим каноническую таблицу для данной функции:
| x (t) | q(t-1) | y(t) | q(t) |
Данная таблица не является таблицей истинности. Преобразуем данную таблицу в таблицу истинности. Для этого значения второго и четвёртого столбца закодируем в двоичной системе счисления:
| x (t) | 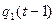 | 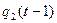 | y(t) | 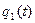 | 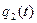 |
| Не определена | |||||
| Не определена |
Доопределим данную функцию следующим образом:
| x (t) | 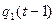 | 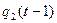 | y(t) | 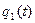 | 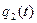 |
Составим канонические уравнения используя аппарат булевой алгебры:
y(t)= 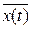
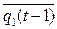
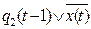
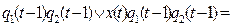
= 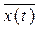
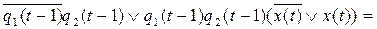
= 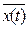
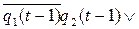
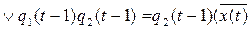
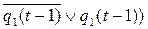
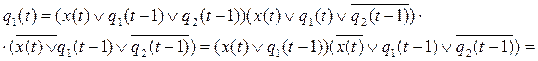
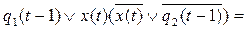
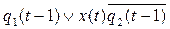
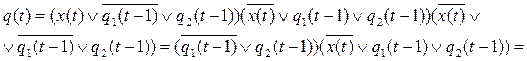
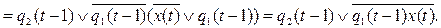
Итак, искомые канонические уравнения имеют вид:
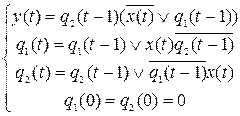
Каждой ограниченно-детерминированной можно сопоставить канонические уравнения. Однако выбор канонических уравнений не однозначен. Эта неоднозначность связана:
1) с различными способами кодирования состояний.
2) с различными способами доопределения функций.
Очевидно, что канонические уравнения позволяют вычислить
по входной последовательности a ={ a (1), a (2),…, a (t),…}
выходную последовательность b ={ b (1), b (2),…, b (t),…}.
Итак, для задания конечного автомата фиксируется три конечных множества (алфавита):
– множество возможных входных сигналов 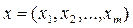
– множество возможных выходных сигналов 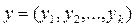
– множество возможных внутренних состояний автомата 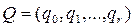 .
.
На этих множествах задаются две детерминированные функции:
– функция переходов Ψ, определяющая состояние автомата q(t) дискретного времени t в зависимости от состояния автомата q(t-1) и значения входного сигнала в момент времени t: q(t)= Ψ(x(t),q(t-1))
– функция выходов Ф, определяющая зависимость выходного сигнала автомата y(t) от состояния автомата q(t-1) и входного сигнала x(t) в момент времени t: y(t)=Ф(x(t),q(t-1)).
Кроме того, на множестве состояний автомата фиксируется одно из внутренних состояний q(0) в качестве начального состояния.
 2015-06-28
2015-06-28 1023
1023
