2015-06-28
3053
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1. 
,
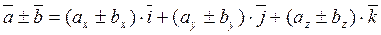или кратко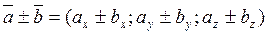 
.
To есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
2. 
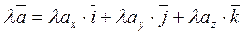или короче λ 
= (λах; λау; λaz). To есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
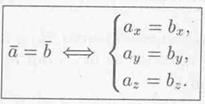
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора u 
равны тогда и только тогда, когда выполняются равенства: ах = bх, ау = bу, аz = bz, т. е.
