1. Скалярное произведение обладает переместительным свойством: 
 =
= 
 .
. 
 =|
=|  | · |
| · |  | •
| • 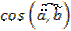 , a
, a 
 = |
= |  |· |
|· |  |·
|· 
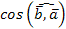 . И так как |
. И так как |  | · |
| · |  | = = |
| = = |  |· |
|· |  |, как произведение чисел и
|, как произведение чисел и 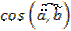 =
= 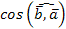 , то
, то 
 =
= 
 .
.
2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: (λ  ) •
) •  = λ(
= λ( 
 ).
).
(λ  ) •
) •  =|
=|  |пр
|пр 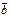 λ
λ  = λ • |
= λ • |  | • пр
| • пр 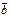
 = λ(
= λ( 
 ).
).
3. Скалярное произведение обладает распределительным свойством:
 (
(  +
+  ) =
) = 
 +
+ 
 .
.
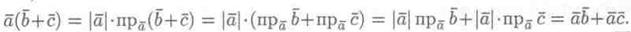
4. Скалярный квадрат вектора равен квадрату его длины:  2 = |
2 = |  |2.
|2.
 2=
2=  •
•  = |
= |  | • |
| • |  |cos 0 = |
|cos 0 = |  | · |
| · |  | = |
| = |  |2
|2
В частности: 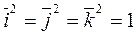
Если вектор  возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль |
возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль |  |, т. е.
|, т. е. 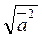 = |
= |  | (
| ( 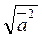 ≠
≠  ).
).
Пример.
Найти длину вектора  = 3
= 3  - 4
- 4  , если |
, если |  | = 2, |
| = 2, |  | = 3,
| = 3, 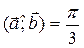 .
.

5. Если векторы  и
и  (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если
(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если 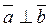 , то
, то 
 = 0. Справедливо и обратное утверждение: если
= 0. Справедливо и обратное утверждение: если 
 = 0 и
= 0 и  ≠
≠ 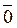 ≠
≠  , то
, то 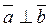 .
.
Так как 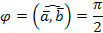 , то cos φ = cos π/2 = 0. Следовательно,
, то cos φ = cos π/2 = 0. Следовательно,  ·
·  =|
=|  |· |
|· |  |·0 = 0. Если же
|·0 = 0. Если же  ·
·  = 0 и |
= 0 и |  | ≠ 0, |
| ≠ 0, |  | ≠ 0, то
| ≠ 0, то 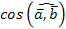 = 0. Отсюда
= 0. Отсюда 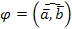 = 90°, т. е.
= 90°, т. е. 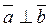 . В частности:
. В частности: 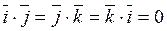
3. Выражение скалярного произведения через координаты
Пусть заданы два вектора
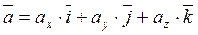 ,
, 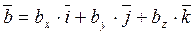
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов единичных 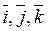 :
:
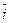 | 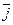 | 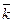 | |
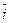 | |||
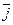 | |||
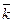 |
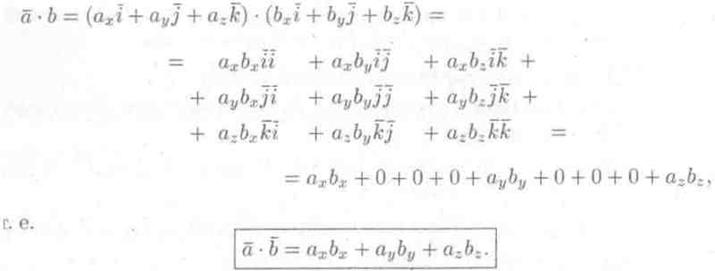
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример 6.2. Доказать, что диагонали четырехугольника, заданного координатами вершин A (-4;-4;4), B (-3;2;2), C (2; 5; 1), D (3;-2;2), взаимно перпендикулярны.
Решение: Составим вектора 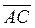 и
и 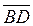 , лежащие на диагоналях данного четырехугольника. Имеем:
, лежащие на диагоналях данного четырехугольника. Имеем: 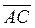 = (6;9;-3) и
= (6;9;-3) и 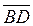 = (6;-4;0). Найдем скалярное произведение этих векторов:
= (6;-4;0). Найдем скалярное произведение этих векторов:
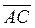 ·
· 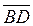 = 36 - 36 - 0 = 0.
= 36 - 36 - 0 = 0.
Отсюда следует, что 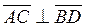 . Диагонали четырехугольника ABCD взаимно перпендикулярны. •
. Диагонали четырехугольника ABCD взаимно перпендикулярны. •
4. Некоторые приложения скалярного произведения
 2015-06-28
2015-06-28 2186
2186
