| Задания 12.Высота конуса равна 7, а диаметр основания – 48. Найдите образующую конуса. | ||
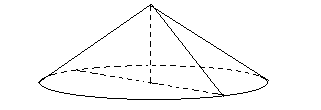
| Решение:
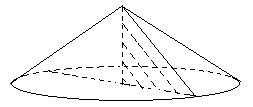 SO – высота конуса, тогда SO – высота конуса, тогда  SOВ –
прямоугольный.
По теореме Пифагора
SВ2 = SО2 + ОВ2,
SВ2 = 72 + (48:2)2,
SВ2 = 49 + 242, SOВ –
прямоугольный.
По теореме Пифагора
SВ2 = SО2 + ОВ2,
SВ2 = 72 + (48:2)2,
SВ2 = 49 + 242,
| S A O 24 B |
SВ2 = 49 + 576, SВ2 = 625,
т.к. SВ  0, тогда образующаяконуса SВ= 25.
В бланк ответов: 25 0, тогда образующаяконуса SВ= 25.
В бланк ответов: 25
|
Пример 13.
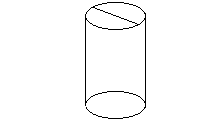 Задание 12.Площадь боковой поверхности цилиндра равна 12 Задание 12.Площадь боковой поверхности цилиндра равна 12 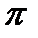 , а высота равна 6. Найдите диаметр основания. , а высота равна 6. Найдите диаметр основания.
| |
Решение:
Площадь боковой поверхности цилиндра 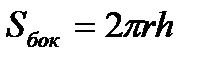 , где , где 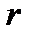 -радиус основания, -радиус основания, 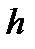 - высота цилиндра. Подставляя в формулу - высота цилиндра. Подставляя в формулу 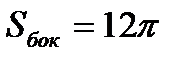 , , 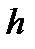 =6, получим =6, получим 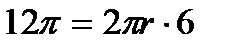 . Диаметр основания d = 2 r, тогда . Диаметр основания d = 2 r, тогда 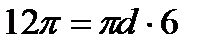 . Отсюда d = 2.
В бланк ответов: 2 . Отсюда d = 2.
В бланк ответов: 2
|
 2015-06-24
2015-06-24 420
420







