Даны векторы 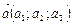 ,
, 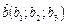 ,
, 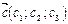 ,
,
т.е. 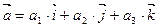 ,
, 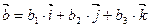 ,
, 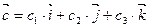
Вычислим смешанное произведение
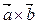 =(
=(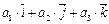 )´(
)´(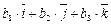 )=
)= 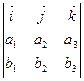 =
= 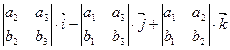
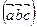 =
= 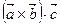 =
= 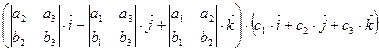 =
=
= 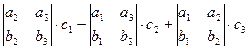 =
= 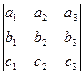 .
.
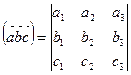 . (8.21)
. (8.21)
Пример 5.
Вычислим объем тетраэдра DАВС: А (1;2;1), В (4;1;2), С (1;5;3), D (2;3;1).
Решение. 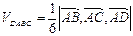 .
.
Найдем координаты 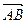 ,
, 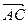 ,
, 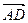 , на которых построен тетраэдр DАВС, как на ребрах:
, на которых построен тетраэдр DАВС, как на ребрах: 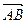 (3;–1;1),
(3;–1;1), 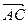 (0;3;2),
(0;3;2), 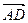 (1;1;0).
(1;1;0).
Вычислим смешанное произведение и объем тетраэдра:
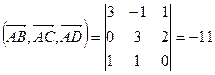
Приложения произведений векторов
| п/п | Вид операции | Приложение |
| Линейная | Условие коллинеарности 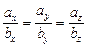 | |
| Скалярное произведение | Условие перпендикулярности векторов: Если 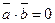 , то векторы перпендикулярны , то векторы перпендикулярны | |
| Скалярное произведение | Вычисление угла между векторами | |
| Векторное произведение | Условие коллинеарности векторов: 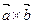 = = 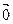 . . | |
| Векторное произведение | Вычисление площади параллелограммов и треугольников, построенных на векторах с общим началом как на сторонах 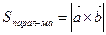 и и 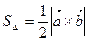 | |
| Векторное произведение | Момент силы 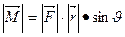 | |
| Смешанное произведение | Вычисление объема параллелепипеда, четырехугольной пирамиды, тетраэдра (треугольной пирамиды), построенных на трех векторах с общим началом, как на ребрах: 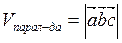 , , 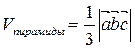 , , 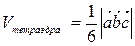 | |
| Смешанное произведение | Определение ориентации векторов в пространстве: Если (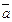 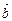  )>0, то тройка векторов )>0, то тройка векторов 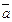 , , 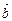 , ,  – правая; если ( – правая; если (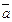 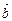  )<0, то тройка векторов )<0, то тройка векторов 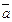 , , 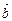 , ,  – левая. – левая. | |
| Смешанное произведение | Условие компланарности трех векторов: Если 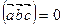 , то векторы , то векторы 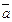 , , 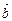 , ,  компланарны. компланарны. | |
| Смешанное произведение | Установление компланарности четырех точек (принадлежности одной плоскости): Если 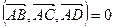 , то точки А, B, C, D лежат в одной плоскости. , то точки А, B, C, D лежат в одной плоскости. | |
 2015-06-28
2015-06-28 4481
4481