Рассмотрим векторно-скалярное произведение векторов  ,
,  и
и  , составленное следующим образом:
, составленное следующим образом: 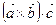 . Первые два вектора умножаются векторно, а их результат на третий вектор скалярно. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов.
. Первые два вектора умножаются векторно, а их результат на третий вектор скалярно. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов.
Определение 31.
Смешанным (векторно-скалярным) произведением трех векторов  ,
,  и
и  называется число
называется число 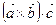 , полученное в результате векторного произведения векторов
, полученное в результате векторного произведения векторов  и
и  , умноженного скалярно на вектор
, умноженного скалярно на вектор  .
.
Обозначение: 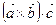 =
= 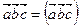 (8.12)
(8.12)
Из определения следует: 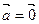 , или
, или 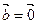 , или
, или 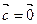 , то
, то 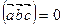 (самостоятельно)
(самостоятельно)
Пример 4. Вычислим смешанное произведение ортов (по определению).
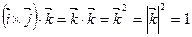 .
.
 2015-06-28
2015-06-28 464
464








