Свойства смешанного произведения. 1. Смешанное произведение не зависит от порядка векторного и скалярного умножения, т.е

1. Смешанное произведение не зависит от порядка векторного и скалярного умножения, т.е. не изменится при перестановке знаков умножения.

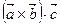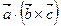= (8.13)

Доказательство.

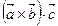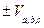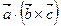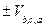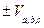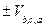= , = , причем одного знака, так как тройки , , и , , – обе правые. Значит, = . Отсюда, = .

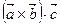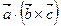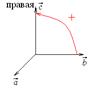
Это свойство позволяет записывать смешанное произведение векторов без знаков векторного и скалярного умножения.

2. Смешанное произведение не изменяется при циклической перестановке множителей:

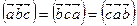(8.14)

Доказательство. 1) 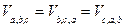; 2) если тройка векторов , , – правая, то тройки , , и , , – тоже правые.

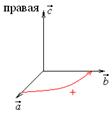
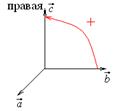
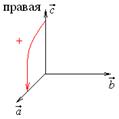
3. Смешанное произведение меняет знак на противоположный при перестановке двух множителей:

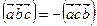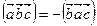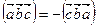, , (8.15)

Доказательство. самостоятельно

1) 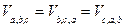; 2) если тройка векторов , , – правая, то тройки , , – левые.

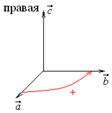
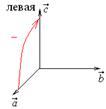
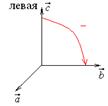
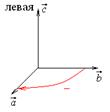
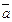
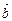
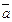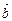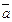
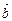
4. Если ( )>0, то тройка векторов , , – правая; если ( )<0, то тройка векторов 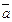, , 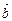– левая.

5. Теорема.

Смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны

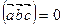(8.16)

Доказательство.

1) Дано: 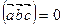. Докажем, что векторы , , компланарны.

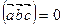Þ 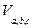= SH =0 Þ а) S =0 или б) Н =0.

а) S =0 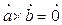Þ Þ , коллинеарны Þ , , компланарны;

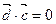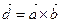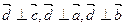б) Н =0 Þ , где Þ Þ , , компланарны.

2) Дано: векторы , , компланарны. Докажем, что .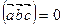

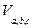=0 Þ .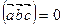

Теорема доказана.

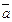
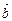
6. Условие компланарности трех векторов: ( )=0.