Даны векторы 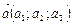 ,
, 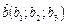 ,
,
т.е. 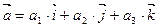 ,
, 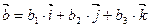
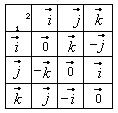
Векторное произведение ортов (см. табл.)
Тогда 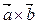 =(
=(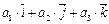 )´(
)´(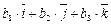 )=
)=
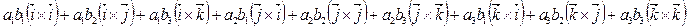 =
=
= 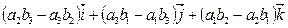 .
.
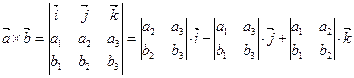 . (8.10)
. (8.10)
17. Геометрический смысл векторного произведения:
1) Площадь параллелограмма. 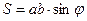 – формула площади параллелограмма.
– формула площади параллелограмма.
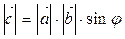 – модуль векторного произведения по определению.
– модуль векторного произведения по определению.
Тогда 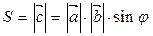 .
.
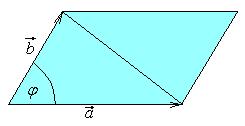
Площадь параллелограмма, построенного на векторах  и
и  как на сторонах, равна модулю векторного произведения этих векторов.
как на сторонах, равна модулю векторного произведения этих векторов.
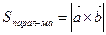 ,
,
2) Площадь треугольника: 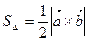 .
.
Площадь треугольника, построенного на векторах  и
и  как на сторонах, равна половине модуля векторного произведения этих векторов.
как на сторонах, равна половине модуля векторного произведения этих векторов.
Пример 2. Вычислим площадь грани АВС тетраэдра DАВС, если А (1;2;1), В (4;1;2), С (1;5;3), D (2;3;1).
Решение. 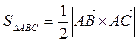 .
.
Найдем координаты 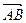 и
и 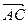 , на которых построен треугольник АВС, как на сторонах:
, на которых построен треугольник АВС, как на сторонах: 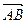 (4–1;1–2;2–1),
(4–1;1–2;2–1), 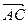 (1–1;5–2;3–1), тогда
(1–1;5–2;3–1), тогда 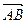 (3;–1;1),
(3;–1;1), 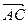 (0;3;2).
(0;3;2).
Вычислим векторное произведение 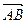 ´
´ 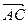 и его длину:
и его длину:
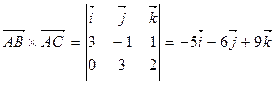
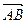 ´
´ 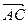 (–5;–6;9),
(–5;–6;9),
| 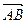 ´
´ 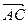 |=
|=  ,
, 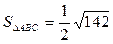 (кв.ед.).
(кв.ед.).
Механический смысл векторного произведения: Моментом силы 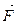 относительно точки О называется вектор
относительно точки О называется вектор 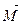 , имеющий начало в точке О, направленный перпендикулярно к плоскости, определяемой точкой О и вектором
, имеющий начало в точке О, направленный перпендикулярно к плоскости, определяемой точкой О и вектором 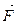 . Длина вектора равна произведению длины вектора
. Длина вектора равна произведению длины вектора 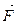 на плечо h – перпендикуляра, опущенного из точки о на направление вектора
на плечо h – перпендикуляра, опущенного из точки о на направление вектора 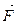 ) или
) или 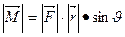 , где
, где 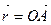 – радиус-вектор точки приложения силы
– радиус-вектор точки приложения силы 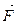 .
.
 2015-06-28
2015-06-28 1208
1208
