Визначимо число r-перестановок з n різних елементів без повторень.
Перестановки. Перший член перестановки можна вибрати з
n елементів n способами – елементи не повинні повторюватися, вибір другого члена можна здійснити n-1 способами і так далі до r-го члена, Якій можна вибрати n-r+1 способами.
Застосовуючи послідовно правило добутку, одержуємо
p(n,r) = n (n-1)......(n – r + 1), n 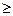 r.
r.
Приклад. З об’єктів 1, 2, 3, 4 можна скласти 12 таких 2-перестановок: 12, 13, 14, 23, 24, 34, 21, 31, 41, 32, 42, 43.
n-перестановки з n різних елементів називають перестановками. Поклавши r = n, маємо число перестановок p(n, n) = 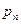 = n(n-1)...2 *1 = n! Використовуючи це співвідношення, можна записати:
= n(n-1)...2 *1 = n! Використовуючи це співвідношення, можна записати:
p(n, r) = 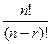 =
= 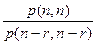 .
.
Розглянемо перестановки з повтореннями з n елементів, специфікація яких { 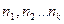 }, причому n =
}, причому n = 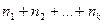 .Через збіг деяких елементів число таких перестановок виявляється менше ніж n!, тому що перестановка однакових елементів нічого не змінює.
.Через збіг деяких елементів число таких перестановок виявляється менше ніж n!, тому що перестановка однакових елементів нічого не змінює.
Перестановки з повтореннями з n елементів: Елементи j-го класу допускають перестановку 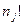 способами, і в кожнім класі такі операції здійснюються незалежно, відповідно до правила добутку можна зробити
способами, і в кожнім класі такі операції здійснюються незалежно, відповідно до правила добутку можна зробити 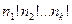 перестановок, що не змінюють дану перестановку.
перестановок, що не змінюють дану перестановку.
Число різних перестановок з повтореннями, що виходять з n елементів, виражається формулою
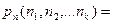
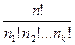
Приклад. План забудови вулиці 10 будинками, серед яких 3 будинки одного типу, 5 - другого і 2 - третього, можна представити 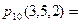 10! 3! 5! 2!= 2520 способами.
10! 3! 5! 2!= 2520 способами.
Якщо запас об'єктів n різних типів не обмежений, то кожне місце в
r-перестановці можна заповнити n різними способами. Тому відповідно до правила добутку число r-перестановок з необмеженими повтореннями дорівнюєU(n, r) = 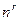 . Це співвідношення, зокрема, визначає кількість різних r-розрядних чисел, записаних у позиційній системі з підставою n.
. Це співвідношення, зокрема, визначає кількість різних r-розрядних чисел, записаних у позиційній системі з підставою n.
 2015-06-28
2015-06-28 460
460








