Рассмотрим два вектора на плоскости 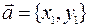 и
и 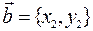 . Эти векторы можно представить как линейные комбинации базисных векторов
. Эти векторы можно представить как линейные комбинации базисных векторов 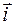 и
и 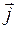 :
:
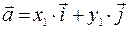
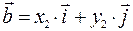
Заметим, что 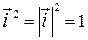 ,
, 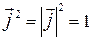 и
и 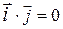 , так как
, так как 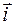 и
и 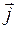 - это единичные и взаимно перпендикулярные векторы.
- это единичные и взаимно перпендикулярные векторы.
Теперь, используя свойства скалярного произведения, получим:
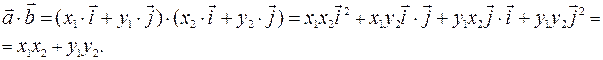
Итак: 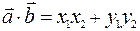
Рассуждая аналогично для векторов в пространстве 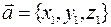 и
и 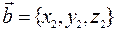 , получим:
, получим:
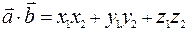
Замечание.
Рассмотрим вектор 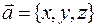 . Очевидно, что
. Очевидно, что 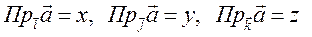 .
.
Отсюда получим, что 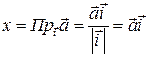 ,
, 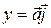 ,
, 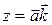 .
.
 2015-06-28
2015-06-28 653
653








