2015-06-28
1882
Сейчас мы рассмотрим специфическую операцию над двумя пространственными векторами. Результатом этой операции будет вектор. Поэтому эта операция называется векторным произведением.
Аналогом этой операции в двумерном пространстве (для векторов плоскости) будет операция, совершаемая над одним вектором, а для 4-мерного пространства – это будет операция, совершаемая над 3-мя векторами.
Определение векторного умножения довольно громоздко, доказательство его свойств весьма трудно, однако формула для координат векторного произведения получается изящной. Все это производит впечатление фокуса. Объяснение «фокуса» в «попятном» изложении материала (как в киноленте, прокручиваемой назад). Более естественным является понятие смешанного произведения трех пространственных векторов, с него и нужно было бы начинать изложение. Однако сам термин смешанное произведение («смесь» векторного и скалярного произведений) и традиция заставляют нас излагать этот материал в таком противоестественном порядке.
Рассмотрим три вектора в пространстве. Говорят, что эти векторы компланарны, если, будучи приведенными в общее начало, они окажутся в одной плоскости.
Тройкой векторов будем называть набор, состоящий из трех векторов, взятых в определенном порядке. Например, тройки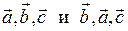 
различны, поскольку различаются порядком следования, хотя и состоят из одних и тех же векторов.
Тройка некомпланарных векторов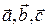 
называется правой тройкой, если, совместив начала векторов в одной точке и наблюдая из конца вектора 
плоскость, "натянутую" на векторы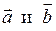 
, обнаруживаем, что вращение вектора 
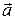по кратчайшему пути до совмещения с линией вектора 
должно происходить против часовой стрелки. Если в указанных выше условиях вращение вектора по кратчайшему пути до совмещения с линией вектора должно происходить по часовой стрелке, то тройка называется левой.
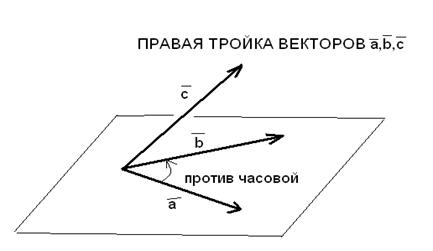
Разведенные пальцы правой руки, взятые в порядке "большой", "указательный", "средний", образуют правую тройку (соответственная тройка пальцев левой руки – левая).
Тройку компланарных векторов будем считать одновременно правой и левой.
Замечание.
Мы везде предполагаем, что декартова координатная система в пространстве правая.
Рассмотрим два вектора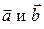 
в пространстве, обозначим буквой 
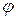угол между ними. Векторное произведение 
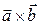(или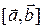 
) двух пространственных векторов 
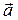и 
– это вектор , обладающий следующими свойствами:
1) 
,
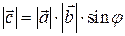т.е. длина вектора равна площади параллелограмма, построенного на векторах 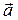и ;
2) вектор перпендикулярен вектору 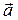и вектору ,
т.е. перпендикулярен плоскости этого параллелограмма (поэтому 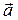· =0, · =0);
3) векторы 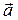, и , взятые в указанном порядке, образуют правую тройку.
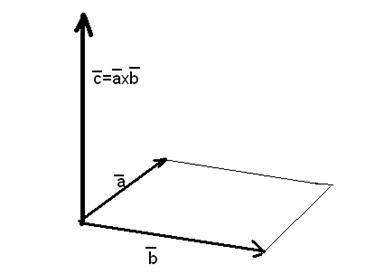
Мы привели рисунок для случая неколлинеарных векторов 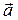и .
Если векторы 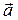и коллинеарны, то 
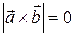, и поэтому 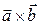будет нулевымвектором. В частности, 
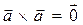для любого вектора .
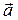Векторное умножение обладает следующими свойствами:
,
,
.
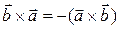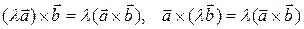Эти свойства выполнены для любых векторов 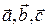и для любого числа 
.
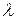Первые два свойства легко доказать. Последнее свойство трудно доказать, опираясь только на геометрическое определение векторного произведения, которое мы дали. Мы докажем это свойство позже.
