Условие компланарности трех векторов.
Рассмотрим правую тройку некомпланарных векторов 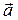 ,
,  ,
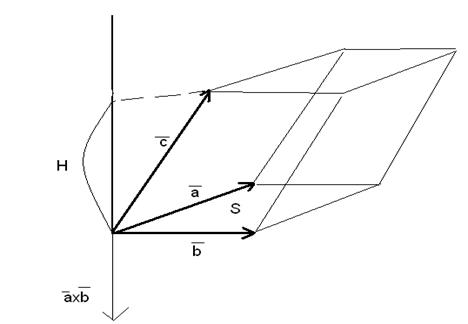
,  . Приведем их в общее начало и построим параллелепипед, в котором векторы
. Приведем их в общее начало и построим параллелепипед, в котором векторы 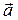 ,
,  ,
,  будут ребрами, выходящими из одной вершины.
будут ребрами, выходящими из одной вершины.
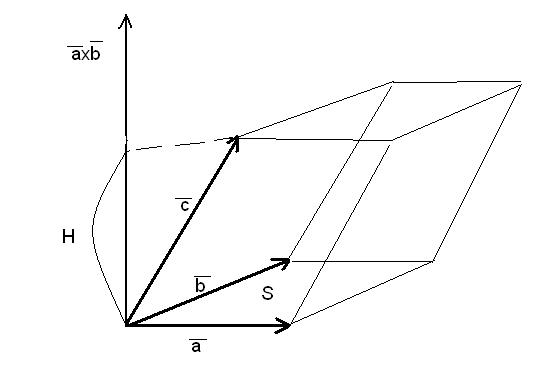
Обозначим буквой 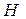 высоту параллелепипеда, буквой
высоту параллелепипеда, буквой 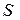 площадь его основания (площадь параллелограмма, построенного на векторах
площадь его основания (площадь параллелограмма, построенного на векторах 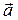 ,
,  ), а буквой
), а буквой 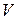 объем параллелепипеда.
объем параллелепипеда.
Далее: 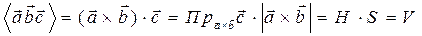 .
.
В случае левой тройки некомпланарных векторов 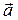 ,
,  ,
,  угол между вектором
угол между вектором  и вектором
и вектором 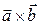 будет тупым, и
будет тупым, и 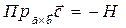 . Поэтому
. Поэтому
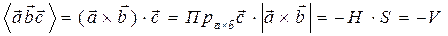
Если векторы 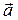 ,
,  ,
,  компланарны, то либо
компланарны, то либо 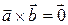 , либо
, либо 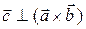 . В обоих случаях
. В обоих случаях 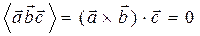 . (Можно также повторить предыдущее геометрическое рассмотрение, считая параллелепипед вырожденным, имеющим нулевую высоту или площадь основания).
. (Можно также повторить предыдущее геометрическое рассмотрение, считая параллелепипед вырожденным, имеющим нулевую высоту или площадь основания).
Итак, мы установили, что смешанное произведение векторов 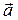 ,
,  ,
,  равно объему параллелепипеда построенного на этих векторах в случае, когда тройка правая, или объему, взятому со знаком минус в случае левой тройки.
равно объему параллелепипеда построенного на этих векторах в случае, когда тройка правая, или объему, взятому со знаком минус в случае левой тройки.
Кроме того, мы получили условие компланарности трех пространственных векторов: векторы 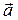 ,
,  ,
,  компланарны тогда и только тогда, когда их смешанное произведение
компланарны тогда и только тогда, когда их смешанное произведение 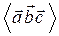 равно нулю.
равно нулю.
Используя это условие компланарности, мы получим, что 4 точки 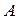 ,
, 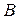 ,
, 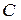 ,
, 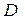 будут лежать в одной плоскости тогда и только тогда, когда
будут лежать в одной плоскости тогда и только тогда, когда 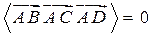 .
.
 2015-06-28
2015-06-28 585
585








