Для объема параллелепипеда построенного на тройке векторов 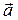 ,
,  ,
,  имеем формулу:
имеем формулу: 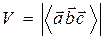 .
.
Объем тетраэдра (треугольной пирамиды).
Рассмотрим треугольную пирамиду 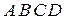 :
:
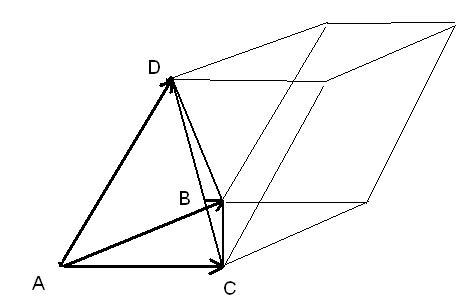
Построим параллелепипед на тройке векторов 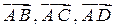 . Заметим, что площадь основания пирамиды в два раза меньше площади основания параллелепипеда, а высоты у них равны. Получаем:
. Заметим, что площадь основания пирамиды в два раза меньше площади основания параллелепипеда, а высоты у них равны. Получаем: 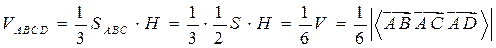
Если тройка 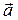 ,
,  ,
,  -правая, то и тройка векторов
-правая, то и тройка векторов  ,
,  ,
, 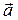 будет правой. Параллелепипед, построенный на тройке
будет правой. Параллелепипед, построенный на тройке  ,
,  ,
, 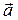 , совпадает с параллелепипедом, построенным на тройке
, совпадает с параллелепипедом, построенным на тройке 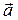 ,
,  ,
,  . Поэтому
. Поэтому
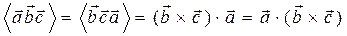 .
.
Теперь мы можем доказать остававшееся недоказанным свойство векторного произведения: 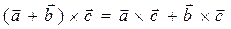 .
.
 2015-06-28
2015-06-28 553
553








