Докажем, что координаты векторов в правой и левой части равенства совпадают.
Первая координата – это проекция на ось абсцисс, она же проекция на вектор 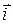 .
.
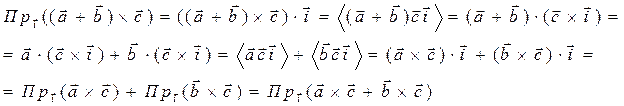 Мы использовали свойства скалярного произведения и проекций.
Мы использовали свойства скалярного произведения и проекций.
Аналогично доказывается равенство вторых и третьих координат. Следовательно, векторы в правой и левой части равенства равны между собой.
Формула для вычисления смешанного произведения векторов, заданных своими координатами
Рассмотрим три пространственных вектора 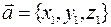 ,
, 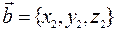 и
и 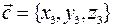 .
.
Вектор 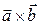 имеет координаты:
имеет координаты: 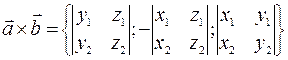 .
.
Используя правило разложения определителя (по третьей строке), получаем:
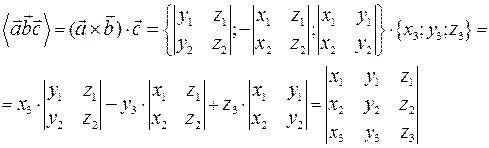
Итак: 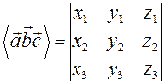 .
.
 2015-06-28
2015-06-28 415
415








