Предположим, что заданы координаты векторов 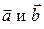 :
:
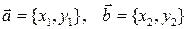 . Тогда
. Тогда
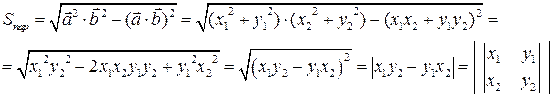
Можно доказать, что 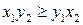 , если пара векторов
, если пара векторов 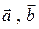 - правая, и
- правая, и 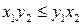 , если пара векторов
, если пара векторов 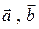 - левая.
- левая.
Аналог смешанного произведения для векторов плоскости
Для векторов на плоскости операция, аналогичная смешанному произведению, будет операцией над двумя векторами.
Если два вектора на плоскости имеют координаты: 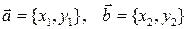 , то естественно определить аналог смешанного произведения как число равное определителю:
, то естественно определить аналог смешанного произведения как число равное определителю:
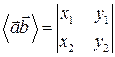
Ввиду доказанной формулы для 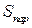 , получим геометрический смысл этой операции:
, получим геометрический смысл этой операции: 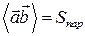 , если пара векторов
, если пара векторов 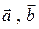 - правая и
- правая и 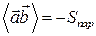 , если эта пара левая.
, если эта пара левая.
Аналогия простирается и дальше на пространство любой размерности.
Задача
Докажите, что аналог векторного произведения для векторов плоскости – это операция, совершаемая над одним вектором 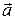 (результат обозначим
(результат обозначим 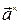 ). Она сводится к повороту этого вектора
). Она сводится к повороту этого вектора 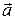 на
на 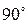 против часовой стрелки.
против часовой стрелки.
Указание
Определите координаты вектора 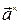 из условия:
из условия:
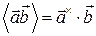 для любого вектора
для любого вектора 
То есть мы как бы «делим» скалярно «смешанное произведение» на вектор  .
.
ЗАДАНИЯ УПРАЖНЕНИЙ
1. Даны координаты точек на плоскости 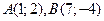 . Найти
. Найти
а) координаты вектора 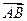 ,
,
б) координаты точки 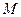 - середины отрезка
- середины отрезка 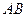 ,
,
в) координаты точки 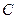 , если
, если 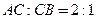 ,
,
г) координаты точки 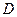 , если
, если 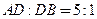 ,
,
д) координаты точки 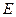 , если
, если 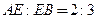 .
.
2. Даны координаты векторов 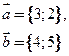
Найти а) координаты 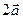 ,
,
б) координаты 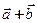 ,
,
в) координаты 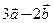 .
.
3. Даны длины векторов и угол между ними 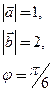
Найти а) скалярное произведение 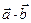 ,
,
в) длину вектора 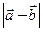 ,
,
г) проекцию вектора на направление другого вектора 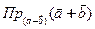 ,
,
д) угол между векторами 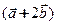 и
и 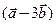 .
.
4. Даны координаты векторов 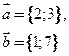
Выполнить задания пунктов а) - д) предыдущей задачи.
5. При каком значении параметра 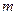 векторы
векторы 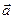 и
и 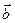 будут перпендикулярны?
будут перпендикулярны?
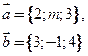
6. При каких значениях 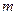 и
и 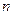 векторы
векторы 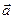 и
и 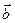 будут параллельны?
будут параллельны?
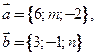
7. Даны длины векторов и угол между ними 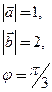
Найти а) длину векторного произведения 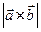 ,
,
б) длину векторного произведения 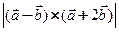 .
.
8. Даны координаты векторов 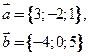
Найти координаты векторного произведения 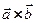 .
.
9. Даны координаты вершин треугольника на плоскости
 . Найти площадь треугольника
. Найти площадь треугольника 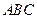 .
.
10. Даны координаты вершин треугольника в пространстве
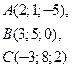 . Найти площадь треугольника
. Найти площадь треугольника 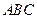 .
.
11. Даны координаты векторов в пространстве 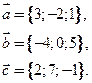
Найти смешанное произведение 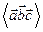 .
.
12. Даны координаты вершин пирамиды в пространстве
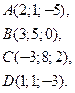 . Найти а) объём пирамиды
. Найти а) объём пирамиды 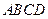 ,
,
б) длину высоты 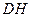 .
.
13. При каком значении параметра 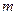 векторы
векторы 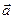 ,
, 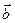 ,
, 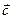 будут компланарны?
будут компланарны?
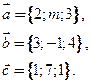
14. При каком значении параметра 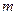 точки
точки 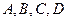 будут лежать в одной плоскости?
будут лежать в одной плоскости? 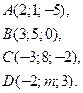
 2015-06-28
2015-06-28 2657
2657

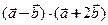 ,
,