Векторы. x, y - координаты вектора

Длина вектора

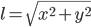
x, y - координаты вектора

Длина пространственного вектора

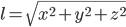
x, y, z - координаты вектора

Скалярное произведение векторов

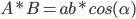
a, b - длины векторов
α - угол между векторами

Скалярное произведение векторов через координаты

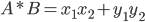
x1, y1 - координаты первого вектора
x2, y2 - координаты второго вектора

Скалярное произведение пространственных векторов через координаты

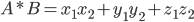
x1, y1, z1 - координаты первого вектора
x2, y2, z2 - координаты второго вектора

Скалярное произведение вертикальных векторов

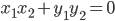
x1, y1 - координаты первого вектора
x2, y2 - координаты второго вектора

Скалярное произведение пространственных вертикальных векторов

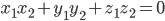
x1, y1, z1 - координаты первого вектора
x2, y2, z2 - координаты второго вектора

Угол между векторами

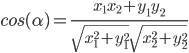
α - угол между векторами
x1, y1 - координаты первого вектора
x2, y2 - координаты второго вектора

Угол между пространственными векторами

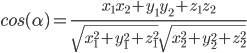
α - угол между векторами
x1, y1, z1 - координаты первого вектора
x2, y2, z2 - координаты второго вектора

Коллинеарные векторы

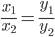
x1, y1 - координаты первого вектора
x2, y2 - координаты второго вектора

Расстояние между точками

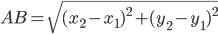
x1, y1 - координаты первой точки
x2, y2 - координаты второй точки

Расстояние между точками в пространстве

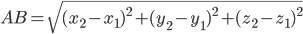
x1, y1, z1 - координаты первой точки
x2, y2, z2 - координаты второй точки

Найти площадь треугольника, координаты вершин которого известны: A (-2, 1, 2); B (3, -3, 4); C (1, 0, 9).

Решение.

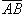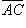Рассмотрим векторы и . Площадь треугольника ABC есть половина площади параллелограмма, построенного на векторах 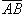и 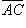. Площадь параллелограмма, построенного на векторах 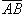и 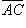, есть модуль векторного произведения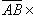 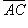, а потому площадь треугольника ABC есть

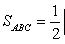
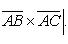
Найти векторное произведение 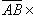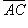, а потом половину его модуля.

Проекции векторов 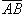и 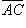на координатные оси найдем по формулам (6):

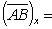
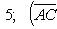
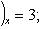
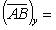
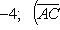
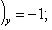
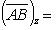
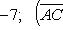
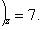
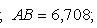
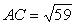
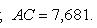
По формуле (27) для векторного произведения векторов найдем, что

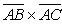
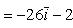
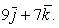
Модуль вектора 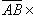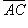найдем по формуле (4):

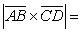
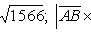
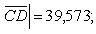
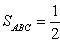
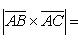
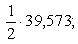
S_ABC = 19,787 кв. ед.