Рассмотренная выше ДПСК является наиболее употребительной. Однако, при решении некоторых задач могут оказаться более удобными и другие системы. Одной их таких СК на плоскости является так называемая полярная СК.
Полярная система координат определяется заданием некоторой точки О (называемой полюсом), луча, исходящего их этой точки (называемого полярной осью) и единичного отрезка для измерения длин. Кроме того, необходимо указать, какие повороты вокруг точки О считаются положительными. Обычно считаются положительными повороты, совершаемые против часовой стрелки.
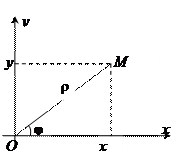
Пусть М – произвольная точка плоскости, на которой задана ПСК. Обозначим через ρ расстояние d (O, M) и через φ – угол, на который
нужно повернуть полярную ось для совмещения ее с лучом ОМ. Угол φ будем понимать так, как это принято в тригонометрии, т.е. с точностью до слагаемого вида ±2nπ.
Полярными координатами точки М называются ρ и φ. При этом число ρ называется полярным радиусом точки М, а число φ – полярным углом. Чтобы избежать неоднозначности будем рассматривать только так называемое главное значение угла φ, т.е. значение, удовлетворяющее соотношению –π<φ≤π или 0≤φ<2π. Тогда каждая точка плоскости характеризуется вполне определенной парой чисел (ρ,φ). Исключение составляет полюс: его полярный угол не имеет определенного значения (полярный радиус равен нулю).
 В случаях, когда приходится одновременно пользоваться и декартовой и полярной системами, возникает необходимость в формулах перехода от одной к другой. В частном
В случаях, когда приходится одновременно пользоваться и декартовой и полярной системами, возникает необходимость в формулах перехода от одной к другой. В частном
случае, когда полюс ПСК совпадает
с началом координат ДПСК, полярная
ось совпадает с положительной полуосью
абсцисс, эти формулы имеют вид
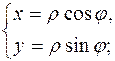
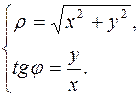
Заметим, что последняя формула для определения значения φ требует знания, в какой четверти находится точка.
 2015-06-28
2015-06-28 751
751








