Определение 1. Скалярным произведением векторов  и
и  называется операция (результат операции), ставящая в соответствии упорядоченной паре векторов
называется операция (результат операции), ставящая в соответствии упорядоченной паре векторов  и
и  скаляр, равный произведению длин векторов на косинус угла между ними.
скаляр, равный произведению длин векторов на косинус угла между ними. 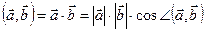 .
.
Замечание. Из определения скалярного произведения, следует, что 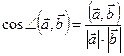 .
.
Замечание. Заметим, что 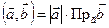 . Если взять вектор
. Если взять вектор  такой, что
такой, что 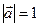 , то
, то 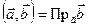 . Таким образом, скалярное произведение одного вектора на другой, имеющий единичную длину, равно проекции первого вектора на направление, определяемое вторым. В этом заключается геометрический смысл скалярного произведения.
. Таким образом, скалярное произведение одного вектора на другой, имеющий единичную длину, равно проекции первого вектора на направление, определяемое вторым. В этом заключается геометрический смысл скалярного произведения.
Замечание. Механический смысл скалярного произведения. Если рассмотреть действия силы 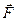 на материальную точку при её перемещении по вектору
на материальную точку при её перемещении по вектору 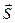 , то работа
, то работа 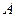 , совершаемая этой силой равна:
, совершаемая этой силой равна: 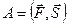 .
.
Свойства скалярного произведения:
1. Коммутативность: 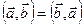 .
.
Доказательство: 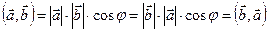 . ■
. ■
2. Унитарность: 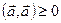 , причём
, причём 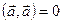 тогда и только тогда, когда
тогда и только тогда, когда 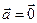 .
.
Доказательство: 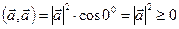 . ■
. ■
3. Однородность: 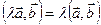 .
.
Доказательство: 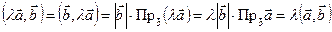 . ■
. ■
4. Дистрибутивность: 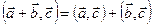 .
.
Доказательство: 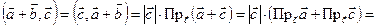
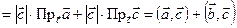 . ■
. ■
Замечание. «однородность + дистрибутивность = линейность».
Теорема1. Критерий ортогональности
Пусть векторы 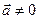 и
и 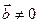 . Тогда
. Тогда 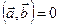 тогда и только тогда, когда
тогда и только тогда, когда 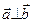 .
.
Пример. В треугольнике 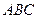 медиана
медиана 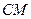 перпендикулярна биссектри
перпендикулярна биссектри 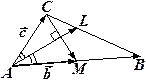 се
се 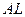 , причём
, причём 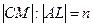 . Найти угол
. Найти угол 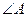 .
.
Решение:
Обозначим 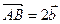 ,
, 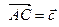 ,
, 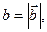
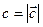 и
и 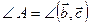 . Тогда
. Тогда 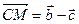 . Выразим
. Выразим 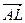 .
.
Известно, что биссектриса угла делит противолежащую сторону в отношении, равном отношении длин прилежащих сторон. Таким образом, 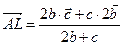 . По условию,
. По условию, 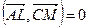 , т.е.
, т.е. 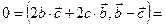
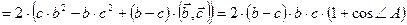 .
.
Так как 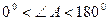 ,
, 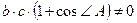 , то
, то 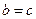 . (В этом можно было убедиться и геометрически: по условию задачи, в
. (В этом можно было убедиться и геометрически: по условию задачи, в 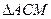 биссектриса
биссектриса 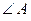 является и высотой, а значит,
является и высотой, а значит, 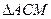 – равнобедренный, т.е.
– равнобедренный, т.е. 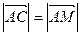 ).
).
Таким образом, 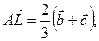
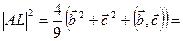
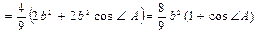 ,
, 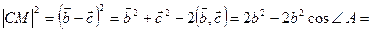
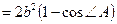 . Следовательно,
. Следовательно, 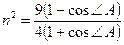 . Отсюда находим
. Отсюда находим 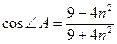 .
.
 2015-06-28
2015-06-28 1676
1676
