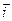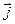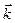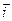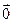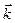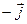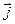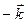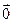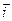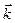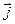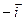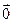Векторное произведение в ДПСК

Рассмотрим векторы 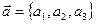и 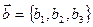в ДПСК 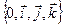. Для базисных векторов 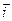, , 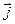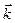имеем: 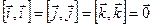, , 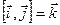, 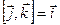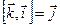или

Тогда в силу линейности векторного произведения

.

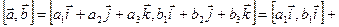
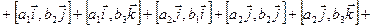
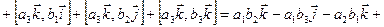
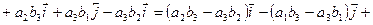
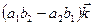Итак, 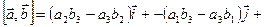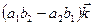. Для запоминания последней формулы удобно использовать псевдоопределитель:

.

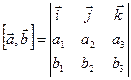Раскрывая этот «определитель», стоящий в правой части, по элементам первой строки, получим разложение вектора 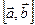по базису .

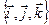Пример. Дан 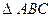. На сторонах треугольника выбраны 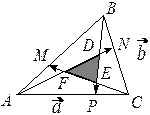соответственно точки 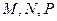так, чтобы 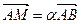, , 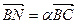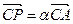. При каком 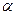площадь 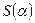треугольника 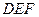наименьшая?

Решение:

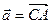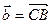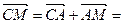
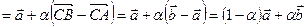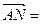
Пусть , . Тогда , 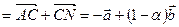. Поэтому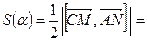 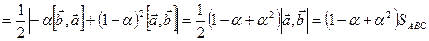Минимум этого выражения достигается при 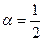, т. е. в случае, когда 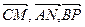- медианы 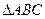. Этот минимум равен .

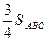П. 11 Произведения тройки векторов