2015-06-28
578
1. Ассоциативность: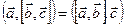 
.
Доказательство:
Очевидно, что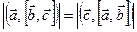 
, так как каждая часть равенства выражает объём параллелепипеда, построенного на векторах 
, 
, 
. Заметим, что обе тройки , , и , , правые, значит
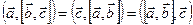в силу коммутативности скалярного произведения. ■
2. Правило циклической перестановки:
.
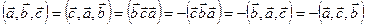Доказательство:
Модули всех этих смешанных произведений равны. Первые три смешанных произведения имеют одну ориентацию, последние три – другую. ■
3. Линейность по каждому аргументу:
,
,
.
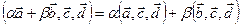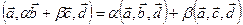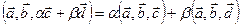| Доказательство: |
Поскольку и скалярные, и векторные произведения однородны и дистрибутивны, т.е. линейны, то и смешанное произведение линейно по всем трем векторам. ■
Теорема 1. К ритерий компланарности векторов
Векторы , 
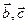компланарны тогда и только тогда, когда их смешанное произведение 
.
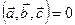Доказательство:
Пусть векторы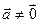 
, 
, 
.
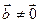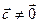Необходимость. Путь векторы , 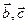компланарны.
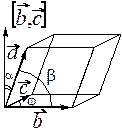По определению они лежат в одной или параллельных плоскостях. Совмести их начала, тогда все три вектора лежат в одной плоскости, отсюда 
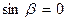. Следовательно, 
.
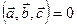Достаточность. Пусть 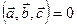. Тогда либо 
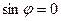, либо 
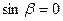. Если 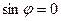, то векторы и коллинеарные, следовательно, векторы , , - компланарны.
Если 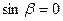, то вектор лежит в той же плоскости, что векторы и , т.е. , , - компланарны. ■
