Определение 1. Рассмотрим некоторую произвольную тройку некомпланарных векторов  ,
,  ,
,  , приведённых к точке
, приведённых к точке 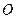 . Тройка векторов
. Тройка векторов 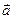 ,
,  ,
,  называется правой, если для неё выполняется правило буравчика: глядя с конца вектора
называется правой, если для неё выполняется правило буравчика: глядя с конца вектора  и
и  , можно увидеть, что кратчайший поворот от
, можно увидеть, что кратчайший поворот от  к
к  происходит против часовой стрелки.
происходит против часовой стрелки.
Определение 2. Векторным произведением векторов называется операция (ре 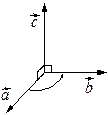 зультат операции), которая любой упорядоченной паре векторов
зультат операции), которая любой упорядоченной паре векторов  и
и  ставит в соответствие вектор
ставит в соответствие вектор 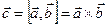 , обладающий следующими свойствами:
, обладающий следующими свойствами:
1) 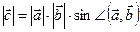 ;
;
2) вектор  ортогонален каждому
ортогонален каждому
из  и
и  ;
;
3)  ,
,  ,
,  – правая тройка;
– правая тройка;
4) если  и
и  - коллинеарные, то
- коллинеарные, то  =
= 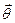 .
.
Замечание. Геометрический смысл векторного произведения двух векто 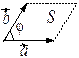 ров
ров  и
и  состоит в том, что модуль
состоит в том, что модуль 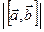 равен площади
равен площади 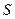 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и  .
.
Замечание. Механический смысл векторного произведения. Если вектор 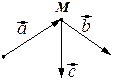
 изображает приложенную в некоторой точке М силу, а вектор
изображает приложенную в некоторой точке М силу, а вектор
 идёт из некоторой точки О в точку М, то вектор
идёт из некоторой точки О в точку М, то вектор 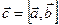 представляет собой момент силы
представляет собой момент силы  относительно точки О.
относительно точки О.
Свойства векторного произведения:
1. Антикоммутативность: 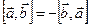 .
.
Доказательство:
Положим 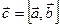 ,
, 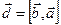 . По определению векторы
. По определению векторы  и
и 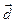 имеют одинаковую длину. Также в силу того, что оба вектора
имеют одинаковую длину. Также в силу того, что оба вектора  и
и 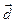 ортогональны к плоскости, определяемой векторами
ортогональны к плоскости, определяемой векторами  и
и  , вектор
, вектор  коллинеарен вектору
коллинеарен вектору 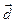 . Тогда либо
. Тогда либо 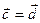 , либо
, либо 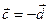 . Если бы имело место первое равенство, то по определению, обе тройки
. Если бы имело место первое равенство, то по определению, обе тройки  ,
,  ,
,  и
и  ,
,  ,
,  оказались бы правыми, но это невозможно. Итак,
оказались бы правыми, но это невозможно. Итак, 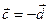 . ■
. ■
2. Однородность: 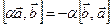 .
.
Доказательство:
Положим 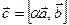 ,
, 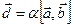 . Пусть векторы
. Пусть векторы  и
и  не коллинеарные и
не коллинеарные и 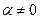 . Обозначим
. Обозначим 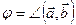 и
и 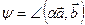 . По определению
. По определению 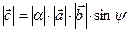 ,
, 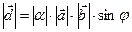 .
.
Возможны два случая:
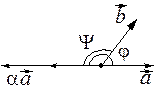
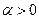 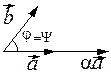 | 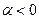 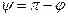 |
| Рис. 2.30 |
В обоих случаях 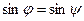 , тогда
, тогда 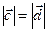 . Далее, заметим, что векторы
. Далее, заметим, что векторы  и
и 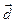 коллинеарные. Остаётся проверить, что эти векторы имеют одинаковое направление.
коллинеарные. Остаётся проверить, что эти векторы имеют одинаковое направление.
Пусть 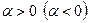 , тогда векторы
, тогда векторы 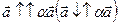 , а значит и векторы
, а значит и векторы 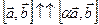
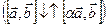 . Итак,
. Итак, 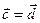 . ■
. ■
3. Дистрибутивность:
Доказательство:
Для доказательства приведём две леммы.
Лемма 1. Векторное произведение произвольного вектора 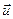 плоскости
плоскости 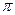 на единичный вектор
на единичный вектор 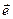 , ортогональный плоскости
, ортогональный плоскости 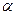 , поворачивает вектор
, поворачивает вектор 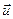 на угол
на угол 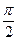 по часовой стрелке, если смотреть с конца вектор
по часовой стрелке, если смотреть с конца вектор 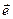 .
.
Доказательство:
По определению 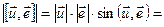
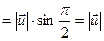 , причём вектор
, причём вектор 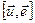 ортогонален векторам
ортогонален векторам 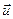 и
и 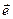 , значит, он лежит на плоскости
, значит, он лежит на плоскости 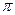 . Тройка векторов
. Тройка векторов 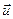 ,
, 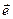 ,
, 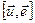 правая, следовательно, поворот от вектора
правая, следовательно, поворот от вектора 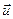 к вектору
к вектору 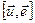 совершается на
совершается на 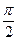 по часовой стрелке, если смотреть с конца вектора
по часовой стрелке, если смотреть с конца вектора 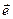 . ■
. ■
Лемма 2. Векторное произведение произвольного вектора 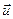 на единичный вектор
на единичный вектор 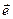 равно
равно 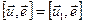 , где
, где 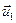 – геометрическая проекция вектора
– геометрическая проекция вектора 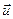 на плоскость
на плоскость 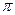 , ортогональную вектору
, ортогональную вектору 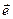 .
.
Доказательство:
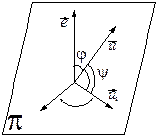 По определению векторного произведения векторы
По определению векторного произведения векторы 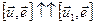 . Рассмотрим их модули:
. Рассмотрим их модули: 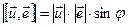 ;
;
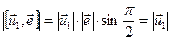 . По условию
. По условию 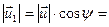
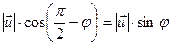 . ■
. ■
Теперь вернёмся к доказательству дистрибутивности 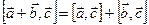 . Для простоты рассмотрим вместо вектора
. Для простоты рассмотрим вместо вектора 
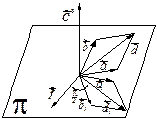 его орт
его орт 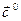 . Пусть векторы
. Пусть векторы  ,
,  ,
,  некомпланарные. Обозначим
некомпланарные. Обозначим 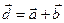 ,
, 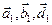 – геометрические проекции векторов
– геометрические проекции векторов 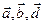 на плоскость
на плоскость 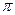 ортогональному вектору
ортогональному вектору  . Тогда по лемме 2 имеем
. Тогда по лемме 2 имеем 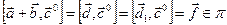 , причём вектор
, причём вектор 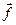 получен поворотом вектора
получен поворотом вектора 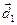 на угол
на угол 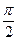 по часовой стрелке (по лемме 1).
по часовой стрелке (по лемме 1).
Аналогично, 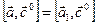 и
и 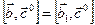 , причём векторы
, причём векторы 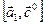 и
и 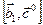 получены поворотами векторов
получены поворотами векторов 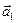 и
и 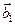 на угол
на угол 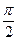 по часовой стрелке, соответственно. Тогда сумма
по часовой стрелке, соответственно. Тогда сумма 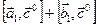 даёт нам вектор
даёт нам вектор 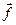 , т.е.
, т.е. 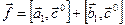 .
.
Таким образом, мы показали, что 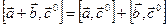 . Умножим обе части равенства на
. Умножим обе части равенства на 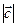 , получим:
, получим: 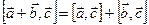 . ■
. ■
Теорема1. Критерий коллинеарности
Векторы  и
и  коллинеарные тогда и только тогда, когда
коллинеарные тогда и только тогда, когда 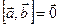 . (доказать самостоятельно)
. (доказать самостоятельно)
 2015-06-28
2015-06-28 10411
10411
